Zadanie nr 7645888
Punkt 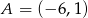 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 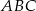 , a punkt
, a punkt 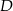 jest środkiem odcinka
jest środkiem odcinka 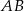 . Równania prostych
. Równania prostych 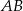 ,
, 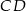 oraz symetralnej boku
oraz symetralnej boku 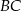 to odpowiednio
to odpowiednio 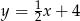 ,
, 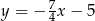 i
i 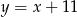 . Napisz równanie prostej zawierającej wysokość trójkąta
. Napisz równanie prostej zawierającej wysokość trójkąta 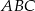 opuszczoną z wierzchołka
opuszczoną z wierzchołka 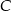 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
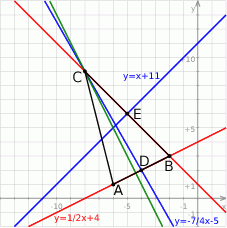
Zacznijmy od wyznaczenia punktu 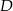 – jest to punkt wspólny podanych prostych
– jest to punkt wspólny podanych prostych 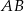 i
i 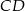 .
.
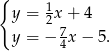
Porównując 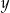 -ki mamy
-ki mamy
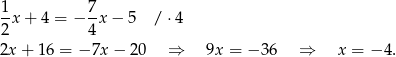
Stąd 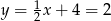 i
i 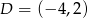 .
.
Wyznaczamy teraz wierzchołek 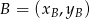 trójkąta
trójkąta 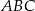 – korzystamy z tego, że
– korzystamy z tego, że 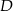 jest środkiem odcinka
jest środkiem odcinka 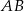 .
.
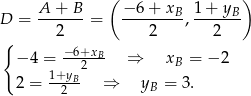
Zatem 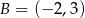 i możemy napisać równanie prostej
i możemy napisać równanie prostej 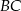 – jest to prosta prostopadła do podanej symetralnej
– jest to prosta prostopadła do podanej symetralnej 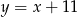 i przechodząca przez
i przechodząca przez 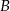 . Szukamy więc prostej w postaci
. Szukamy więc prostej w postaci 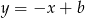 i podstawiamy współrzędne punktu
i podstawiamy współrzędne punktu 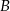 .
.
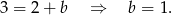
Zatem prosta 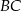 ma równanie
ma równanie 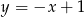 i możemy wyznaczyć współrzędne punktu
i możemy wyznaczyć współrzędne punktu 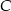 – jest to punkt wspólny prostych
– jest to punkt wspólny prostych 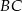 i
i 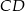 .
.
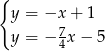
Porównujemy 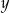 -ki.
-ki.
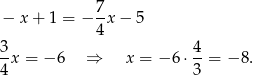
Stąd 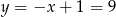 i
i 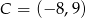 . Pozostało teraz napisać równanie wysokości opuszczonej z wierzchołka
. Pozostało teraz napisać równanie wysokości opuszczonej z wierzchołka 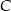 . Jest to prosta prostopadła do
. Jest to prosta prostopadła do 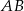 i przechodząca przez
i przechodząca przez 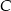 . Szukamy równania w postaci
. Szukamy równania w postaci 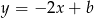 i podstawiamy współrzędne punktu
i podstawiamy współrzędne punktu 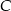 .
.
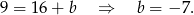
Interesująca nas wysokość ma więc równanie 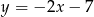 .
.
Odpowiedź: