/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7723898

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są punkty 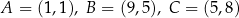A = (1,1), B = (9,5), C = (5,8) .

  • Wyznacz punkt 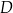D tak, aby czworokąt 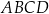ABCD był trapezem prostokątnym, którego kąt przy wierzchołku 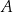A jest prosty.

  • Czy w ten trapez można wpisać okrąg?

Rozwiązanie

Zaczynamy oczywiście od schematycznego rysunku.

ZINFO-FIGURE

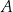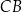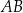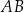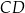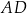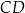  • Skoro kąt prosty ma być przy wierzchołku A , a z obrazka widać, że bok CB nie jest prostopadły do AB więc równoległe muszą być boki AB i CD . Napiszemy teraz równania prostych AD i CD , a potem znajdziemy ich punkt wspólny.

    Prosta 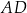AD jest prostopadła do 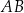AB i przechodzi przez punkt 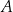A . Najprostszy sposób napisania równania takiej prostej to skorzystanie ze wzoru na równanie prostej prostopadłej do wektora → v = [p,q] i przechodzącej przez punkt (x0,y0) :

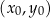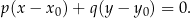
    p(x − x0) + q(y − y0) = 0 .

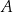    W naszej sytuacji mamy → →v = AB = [8,4] , a punkt to A . Zatem prosta 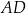AD ma równanie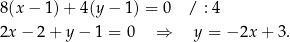

    8(x − 1) + 4(y − 1) = 0 / : 4 2x − 2 + y − 1 = 0 ⇒ y = − 2x + 3.

    Prosta 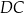DC jest prostopadła do 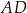AD , zatem jest postaci 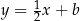y = 1x+ b 2 . Współczynnik 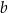b wyliczamy podstawiając współrzędne punktu C .

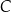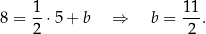
    1- 11- 8 = 2 ⋅5 + b ⇒ b = 2 .

    Szukamy teraz punktu wspólnego otrzymanych prostych

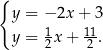
    { y = − 2x+ 3 1 11 y = 2x + 2 .

    Porównując 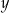y -ki mamy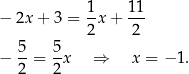

    1- 11- − 2x + 3 = 2 x+ 2 5 5 − --= --x ⇒ x = − 1. 2 2

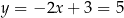    Zatem y = − 2x + 3 = 5 .  
    Odpowiedź: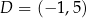 D = (− 1,5)

  • Musimy sprawdzić, czy sumy długości przeciwległych boków są sobie równe. Liczymy

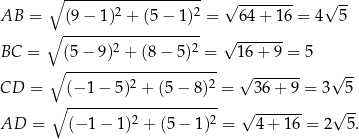
    ∘ ------------------- √ -------- √ -- AB = (9 − 1)2 + (5− 1)2 = 64 + 16 = 4 5 ∘ ------------------- 2 2 √ ------- BC = ∘ (5−--9)-+--(8−--5)-=- 16 + 9 = 5 2 2 √ ------- √ -- CD = (− 1 − 5) + (5 − 8) = 36 + 9 = 3 5 ∘ --------------------- √ ------- √ -- AD = (− 1 − 1)2 + (5 − 1)2 = 4 + 16 = 2 5.

    Teraz widać, że

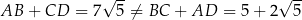
    √ -- √ -- AB + CD = 7 5 ⁄= BC + AD = 5 + 2 5

    (prawa strona jest zdecydowanie mniejsza).  
    Odpowiedź: Nie, nie można.

Wersja PDF