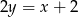Zadanie nr 7896550
Znajdź równania stycznych do okręgu 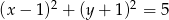 poprowadzonych z punktu
poprowadzonych z punktu 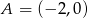 .
.
Rozwiązanie
Sposób I
Zaczynamy od rysunku.
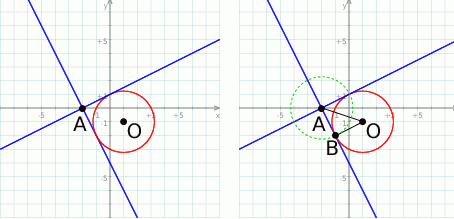
Proste przechodzące przez punkt 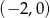 są postaci
są postaci 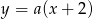 (w zasadzie jest jedna prosta
(w zasadzie jest jedna prosta 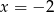 , która nie jest tej postaci, ale z rysunku widać, że nie jest ona szukaną styczną). Wśród tych prostych musimy znaleźć takie, które mają dokładnie jeden punkt wspólny z danym okręgiem. Mamy więc równanie
, która nie jest tej postaci, ale z rysunku widać, że nie jest ona szukaną styczną). Wśród tych prostych musimy znaleźć takie, które mają dokładnie jeden punkt wspólny z danym okręgiem. Mamy więc równanie
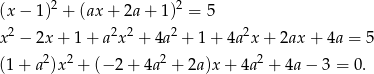
Równanie to ma jedno rozwiązanie jeżeli 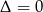 , czyli
, czyli
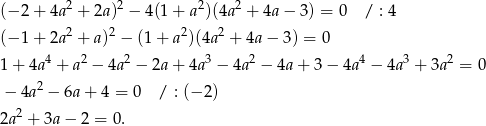
Dalej 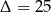 ,
, 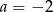 lub
lub 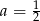 . Stąd szukane styczne to
. Stąd szukane styczne to 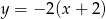 i
i 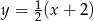 .
.
Powyższe rachunki byłyby znacznie prostsze, gdybyśmy proste sparametryzowali w postaci 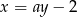 .
.
Sposób II
Tak jak w poprzednim sposobie szukamy stycznych w postaci
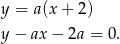
Prosta tej postaci będzie styczna do danego okręgu, gdy jej odległość od punktu 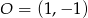 będzie równa promieniowi okręgu, czyli
będzie równa promieniowi okręgu, czyli 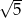 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 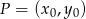 od prostej
od prostej 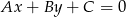 :
:
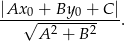
W naszej sytuacji mamy
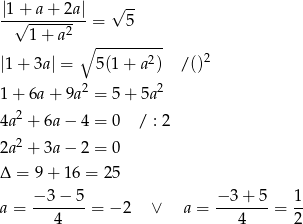
Stąd szukane styczne to 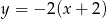 i
i 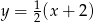 .
.
Sposób III
Tym razem użyjemy odrobinę więcej geometrii. Z trójkąta prostokątnego 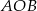 możemy wyliczyć odległość
możemy wyliczyć odległość 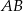 .
.
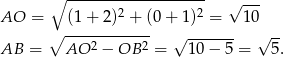
Aby wyznaczyć punkty styczności szukanych stycznych z okręgiem musimy znaleźć punkty wspólne podanego okręgu i okręgu o środku 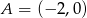 i promieniu
i promieniu 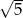 .
.
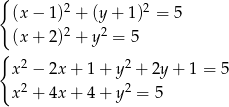
Odejmujemy od pierwszego równania drugie (żeby skrócić kwadraty) i mamy

Wstawiamy to do drugiego równania okręgu.
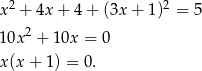
Zatem punkty styczności stycznych to 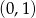 i
i 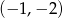 . Pozostało napisać równania stycznych. Można je odgadnąć lub skorzystać ze wzoru na równanie prostej przechodzącej przez dwa punkty
. Pozostało napisać równania stycznych. Można je odgadnąć lub skorzystać ze wzoru na równanie prostej przechodzącej przez dwa punkty 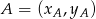 i
i 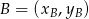 :
:
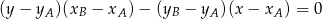
W naszej sytuacji mamy
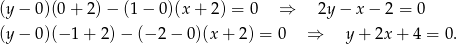
Odpowiedź: 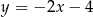 i
i