/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7901311

Dodaj do ulubionych
Dodaj do rozwiązanych

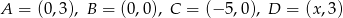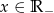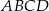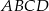Punkty A = (0,3), B = (0,0), C = (− 5,0), D = (x,3) , gdzie x ∈ R − są kolejnymi wierzchołkami czworokąta ABCD . Oblicz wartość x , dla której w czworokąt ABCD można wpisać okrąg.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

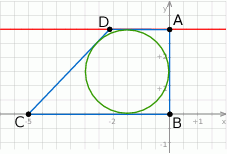
W czworokąt 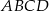ABCD można wpisać okrąg wtedy i tylko wtedy, gdy 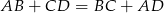AB + CD = BC + AD . Sprawdźmy kiedy tak jest.

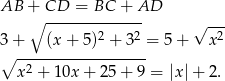
AB + CD = BC + AD ∘ -------------- √ --- 3+ (x + 5)2 + 32 = 5 + x2 ∘ ------------------ x2 + 10x + 25 + 9 = |x |+ 2.

Ponieważ z założenia 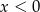x < 0 , mamy 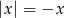|x| = −x i prawa strona jest automatycznie dodatnia. Możemy więc równanie podnieść stronami do kwadratu.

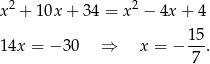
x2 + 10x + 34 = x 2 − 4x + 4 14x = − 30 ⇒ x = − 15-. 7

 
Odpowiedź: x = − 175

Wersja PDF