Zadanie nr 7911771
Znajdź równania prostych stycznych do dwóch okręgów: 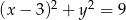 i
i 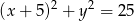 .
.
Rozwiązanie
Zaczynamy od rysunku.
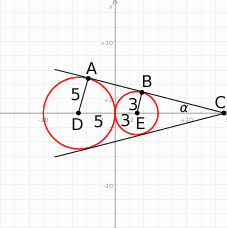
Z rysunku widać, że będą 3 styczne do danych okręgów: prosta 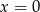 i jeszcze dwie styczne symetryczne względem osi
i jeszcze dwie styczne symetryczne względem osi 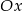 . Zajmiemy się teraz wyznaczeniem tej stycznej od okręgów powyżej osi
. Zajmiemy się teraz wyznaczeniem tej stycznej od okręgów powyżej osi 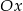 .
.
Trójkąty 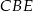 i
i 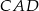 są podobne i łatwo z tego podobieństwa wyliczyć położenie punktu
są podobne i łatwo z tego podobieństwa wyliczyć położenie punktu 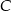 :
:
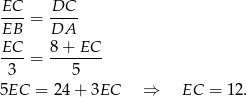
Zatem 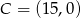 . Z trójkąta
. Z trójkąta 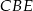 możemy też łatwo wyliczyć
możemy też łatwo wyliczyć 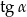 , co pozwoli nam wyznaczyć współczynnik kierunkowy szukanej stycznej.
, co pozwoli nam wyznaczyć współczynnik kierunkowy szukanej stycznej.
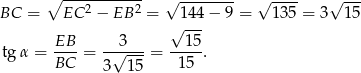
Obliczony tangens to nie jest współczynnik kierunkowy górnej stycznej, bo współczynnik kierunkowy to tangens kąta jaki prosta tworzy z dodatnią półosią 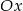 , który jest równy
, który jest równy 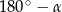 . Obliczony tangens różni się tylko znakiem od interesującego nas współczynnika kierunkowego. Zatem górna styczna jest postaci
. Obliczony tangens różni się tylko znakiem od interesującego nas współczynnika kierunkowego. Zatem górna styczna jest postaci 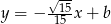 . Współczynnik
. Współczynnik 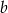 wyliczamy z tego, że prosta ta ma przechodzić przez punkt
wyliczamy z tego, że prosta ta ma przechodzić przez punkt 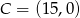 .
.
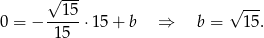
Zatem styczne mają równania
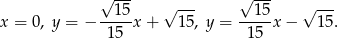
Odpowiedź: