Zadanie nr 7924049
Okrąg o równaniu 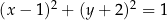 przecina jedną z gałęzi hiperboli o równaniu
przecina jedną z gałęzi hiperboli o równaniu 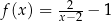 , gdzie
, gdzie 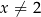 , w punktach
, w punktach 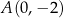 i
i 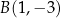 .
.
-
Narysuj obie krzywe we wspólnym układzie współrzędnych.
-
Na drugiej gałęzi hiperboli wyznacz współrzędne takiego punktu
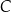 , który jest równo odległy od punktów
, który jest równo odległy od punktów 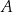 i
i 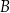 .
.
Rozwiązanie
Okrąg 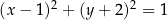 ma środek w punkcie
ma środek w punkcie 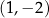 i promień 1. Hiperbola
i promień 1. Hiperbola 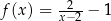 powstaje ze zwykłej hiperboli
powstaje ze zwykłej hiperboli 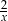 przez przesunięcie o wektor
przez przesunięcie o wektor ![[2,− 1]](https://img.zadania.info/zad/7924049/HzadR4x.png) (czyli przesunięcie o dwie jednostki w prawo i jedną w dół). Korzystając z tych informacji możemy naszkicować rysunek.
(czyli przesunięcie o dwie jednostki w prawo i jedną w dół). Korzystając z tych informacji możemy naszkicować rysunek.
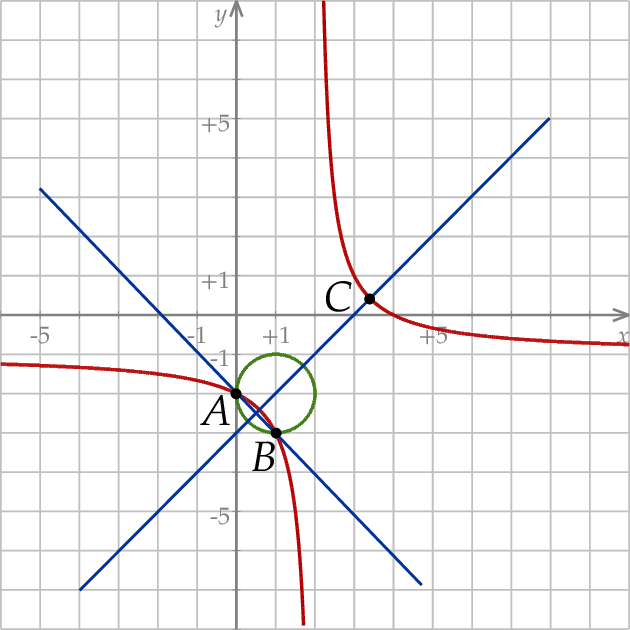
Sposób I
Plan jest następujący. Wyliczymy symetralną odcinka 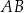 (czyli zbiór punktów, które są w równej odległości od
(czyli zbiór punktów, które są w równej odległości od 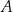 i
i 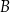 ) i znajdziemy jej punkt przecięcia z drugą gałęzią hiperboli.
) i znajdziemy jej punkt przecięcia z drugą gałęzią hiperboli.
Aby wyliczyć symetralną odcinka 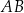 , piszemy wektor
, piszemy wektor ![AB = [1,− 1]](https://img.zadania.info/zad/7924049/HzadR10x.png) . Środek
. Środek 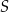 odcinka
odcinka 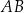 jest równy
jest równy
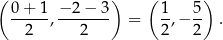
Równanie prostej prostopadłej do wektora ![[v1,v2]](https://img.zadania.info/zad/7924049/HzadR14x.png) i przechodzącej przez punkt
i przechodzącej przez punkt 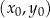 to
to
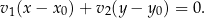
W naszej sytuacji mamy
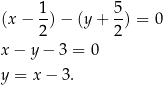
Jeżeli ktoś nie chce korzystać z powyższego wzoru, to może zamiast niego napisać równanie prostej 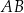 , a potem prostej prostopadłej do
, a potem prostej prostopadłej do 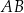 i przechodzącej przez punkt
i przechodzącej przez punkt 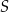 .
.
Pozostało rozwiązań układ równań
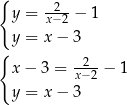
co prowadzi do równania
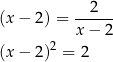
Czyli 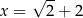 lub
lub 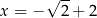 . Jeżeli punkt ma być na prawej gałęzi hiperboli, to musi spełniać
. Jeżeli punkt ma być na prawej gałęzi hiperboli, to musi spełniać 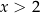 . Otrzymujemy stąd, że szukany punkt to
. Otrzymujemy stąd, że szukany punkt to 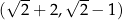 (bo
(bo 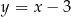 ).
).
Sposób II
Tym razem przyjmijmy, że 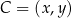 i sprawdzimy kiedy
i sprawdzimy kiedy 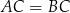 . Ponieważ punkt
. Ponieważ punkt 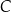 leży na hiperboli, mamy
leży na hiperboli, mamy
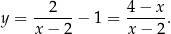
Sprawdźmy teraz kiedy 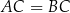 . Od razu porównujemy kwadraty odległości.
. Od razu porównujemy kwadraty odległości.
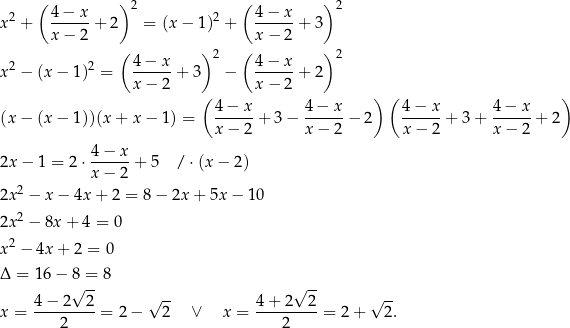
Jak w poprzednim sposobie zauważamy, że musi być 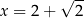 . Stąd
. Stąd
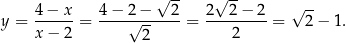
Odpowiedź: