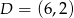/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7956743

Dodaj do ulubionych
Dodaj do rozwiązanych

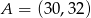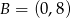Punkty A = (30,3 2) i B = (0,8 ) są sąsiednimi wierzchołkami czworokąta 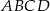ABCD wpisanego w okrąg. Prosta o równaniu 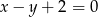x − y + 2 = 0 jest jedyną osią symetrii tego czworokąta i zawiera przekątną AC . Oblicz współrzędne wierzchołków C i D tego czworokąta.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

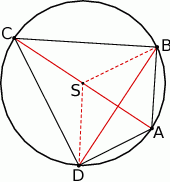
Zauważmy na początek, że łatwo jest napisać równanie przekątnej 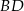BD . Jest ona prostopadła do przekątnej 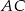AC , więc ma równanie postaci 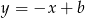y = −x + b . Ponadto przechodzi przez punkt 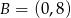B = (0,8) , więc ma równanie y = −x + 8 .

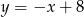Sposób I

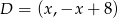Wyznaczamy najpierw współrzędne wierzchołka D . Leży on na przekątnej BD , więc ma współrzędne postaci D = (x,−x + 8) . Ponadto wiemy, że 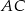AC jest osią symetrii czworokąta, więc

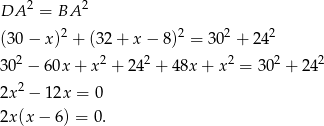
2 2 DA = BA (30− x)2 + (32 + x − 8)2 = 302 + 242 2 2 2 2 2 2 30 − 60x + x + 24 + 48x + x = 30 + 24 2x2 − 12x = 0 2x(x − 6) = 0 .

Rozwiązanie 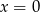x = 0 daje nam punkt 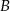B , więc 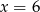x = 6 i

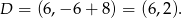
D = (6 ,−6 + 8 ) = (6,2).

Wierzchołek 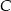C leży na przekątnej 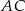AC , więc ma współrzędne postaci 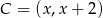C = (x,x + 2) . Ponadto trójkąt 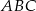ABC jest prostokątny (bo 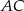AC jest średnicą okręgu), więc

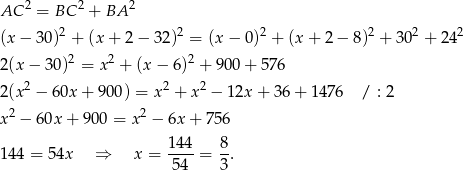
2 2 2 AC = BC + BA (x − 30 )2 + (x + 2 − 32 )2 = (x− 0)2 + (x+ 2− 8)2 + 3 02 + 2 42 2 2 2 2(x − 3 0) = x + (x − 6) + 900 + 576 2(x 2 − 6 0x+ 900) = x 2 + x 2 − 12x + 36+ 1476 / : 2 x2 − 60x + 900 = x2 − 6x + 7 56 144 8 14 4 = 54x ⇒ x = ----= --. 54 3

Stąd

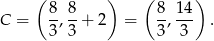
( ) ( ) C = 8, 8+ 2 = 8, 1-4 . 3 3 3 3

Sposób II

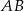Wyznaczmy środek okręgu opisanego na czworokącie ABCD – jest to punkt wspólny osi symetrii czworokąta oraz symetralnej boku AB . Symetralna boku AB to zbiór punktów M = (x,y) , które spełniają warunek

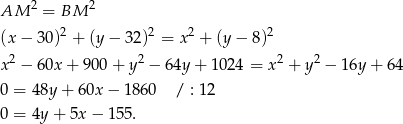
2 2 AM = BM (x − 3 0)2 + (y − 3 2)2 = x2 + (y− 8)2 2 2 2 2 x − 6 0x+ 900 + y − 64y + 10 24 = x + y − 16y + 64 0 = 48y + 60x − 1 860 / : 12 0 = 4y + 5x − 155 .

Szukamy teraz punktu wspólnego tej symetralnej i danej osi symetrii czworokąta.

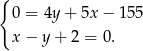
{ 0 = 4y + 5x − 1 55 x − y + 2 = 0.

Podstawiamy 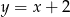y = x+ 2 z drugiego równania do pierwszego i mamy

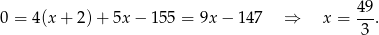
49 0 = 4 (x+ 2)+ 5x− 155 = 9x − 147 ⇒ x = --. 3

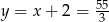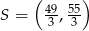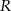Stąd 55 y = x + 2 = 3 i ( 49 55) S = 3 , 3 . Promień R okręgu opisanego na czworokącie ABCD spełnia więc warunek

( ) ( ) 2 2 49- 2 55- 2 2-401 96-1 33-62 R = SB = 0− 3 + 8− 3 = 9 + 9 = 9 .

Szukamy teraz współrzędnych wierzchołka 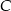C . Leży on na prostej 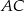AC , więc ma współrzędne postaci 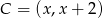C = (x ,x+ 2) . Ponadto spełnia warunek

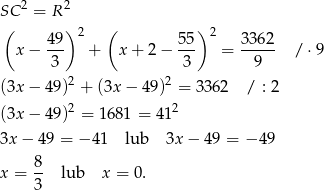
SC 2 = R 2 ( )2 ( )2 49- 55- 3362- x − 3 + x + 2 − 3 = 9 / ⋅9 2 2 (3x − 49) + (3x − 49) = 3362 / : 2 (3x − 49)2 = 1 681 = 412 3x − 49 = − 4 1 lub 3x− 49 = − 49 8 x = -- lub x = 0. 3

Drugie rozwiązanie daje nam punkt 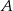A , więc 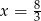x = 8 3 i

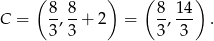
( ) ( ) 8- 8- 8-1-4 C = 3, 3 + 2 = 3, 3 .

Wierzchołek 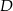D leży na prostej 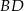BD , więc ma współrzędne postaci 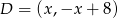D = (x ,−x + 8 ) . Ponadto spełnia warunek

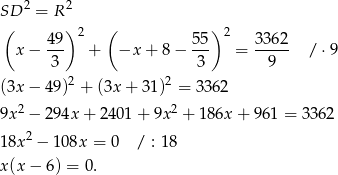
2 2 SD = R ( 49 ) 2 ( 55 )2 3362 x − --- + −x + 8 − --- = ----- / ⋅9 3 3 9 (3x − 49)2 + (3x + 31 )2 = 3362 2 2 9x − 294x + 2401 + 9x + 186x + 961 = 336 2 18x2 − 108x = 0 / : 18 x(x − 6) = 0 .

Rozwiązanie 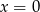x = 0 daje nam punkt 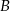B , więc 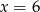x = 6 i

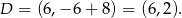
D = (6 ,−6 + 8 ) = (6,2).

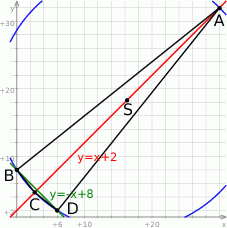
Na koniec dokładny rysunek sytuacji z treści zadania.

PIC

 
Odpowiedź: 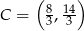( ) C = 8, 14 3 3 , D = (6,2)

Wersja PDF