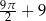Zadanie nr 8015459

Dane są ﬁgury:

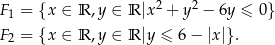
2 2 F1 = {x ∈ R ,y ∈ R|x + y − 6y ≤ 0} F2 = {x ∈ R ,y ∈ R|y ≤ 6 − |x|}.

Narysuj ﬁ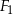gury i 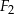oraz wyznacz ﬁgurę .
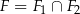Oblicz pole ﬁgury

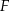
Rozwiązanie

Ponieważ

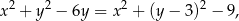
2 2 2 2 x + y − 6y = x + (y − 3) − 9,

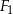ﬁgura F 1 jest wnętrzem okręgu o środku 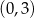(0 ,3) i promieniu 3.

Druga ﬁgura to wszystko co znajduje się pod wykresem funkcji 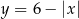y = 6− |x| . Funkcja ta to 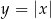y = |x| odbita względem osi 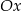i przesunięta o 6 jednostek w górę.

Bez trudu teraz rysujemy obie ﬁgury i zaznaczamy część wspólną.

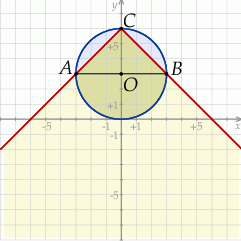
Odpowiedź: Rysunek
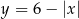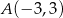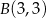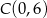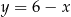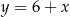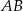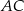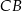Z rysunku widać, że funkcja przecina okrąg w punktach , i . Jeżeli chcielibyśmy to wyliczyć a nie odczytywać z wykresu, to wystarczy wziąć prawy kawałek wykresu funkcji i wstawić do równania okręgu i rozwiązać otrzymane równanie; podobnie dla lewej części wykresu . Ponieważ jest średnicą okręgu, pole niebieskich odcinków kołowych (opartych na łukach i jest równe różnicy pola połowy okręgu i trójkąta 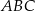, czyli jest równe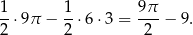
$1-⋅9π − 1-⋅6 ⋅3 = 9-π − 9. 2 2 2$

Wyliczone pole to dokładnie tyle ile trzeba odjąć od pola całego koła aby otrzymać pole .

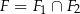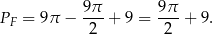
$9π 9π PF = 9 π − --- + 9 = ---+ 9. 2 2$

Odpowiedź: