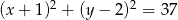/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8076188

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie okręgu opisanego na prostokącie 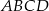ABCD , w którym 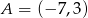A = (− 7,3) i C = (5,1) .

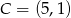Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

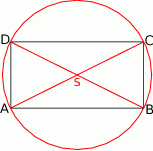
Środkiem okręgu opisanego na prostokącie 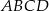ABCD jest środek przekątnej 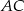AC , czyli punkt

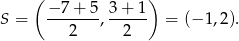
( ) S = −-7-+-5, 3-+-1 = (− 1,2). 2 2

Promień okręgu opisanego to dokładnie długość odcinka 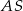AS , czyli

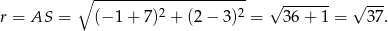
∘ --------------------- r = AS = (− 1 + 7)2 + (2 − 3)2 = √ 36-+-1-= √ 37.

Zatem równanie okręgu opisanego na prostokącie 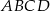ABCD ma postać

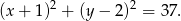
2 2 (x + 1) + (y − 2) = 37.

 
Odpowiedź: (x + 1)2 + (y − 2)2 = 37

Wersja PDF