Zadanie nr 8077442
Dane są punkty 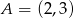 i
i 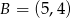 . Na prostej o równaniu
. Na prostej o równaniu 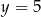 wyznacz punkt
wyznacz punkt 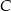 tak, aby łamana
tak, aby łamana 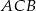 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij.
Rozwiązanie
Skorzystamy z faktu, że jeżeli mamy dwa punkty 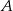 i
i 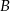 po jednej stronie prostej, to punkt
po jednej stronie prostej, to punkt 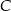 na tej prostej, dla którego łamana
na tej prostej, dla którego łamana 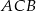 jest najkrótsza to punkt, dla którego kąty jakie tworzą odcinki
jest najkrótsza to punkt, dla którego kąty jakie tworzą odcinki 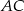 i
i 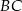 z daną prostą są równe (rysunek).
z daną prostą są równe (rysunek).
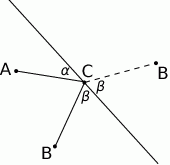
Uzasadnienie tego jest proste, jeżeli 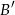 jest obrazem punktu
jest obrazem punktu 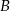 w symetrii względem danej prostej, to
w symetrii względem danej prostej, to
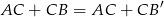
i ta ostatnia liczba jest najmniejsza, gdy punkty 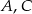 i
i 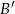 leżą na jednej prostej, co sprowadza się do warunku
leżą na jednej prostej, co sprowadza się do warunku 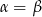 .
.
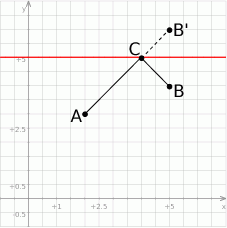
W sytuacji naszego zadania, sprawa jest wyjątkowo prosta, bo prosta jest pozioma, więc łatwo jest znaleźć obraz punktu 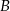 przy symetrii względem tej prostej:
przy symetrii względem tej prostej: 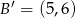 . Napiszemy teraz równanie prostej
. Napiszemy teraz równanie prostej 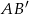 i znajdziemy jej punkt
i znajdziemy jej punkt 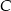 wspólny z prostą
wspólny z prostą 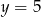 .
.
Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 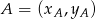 i
i 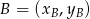 :
:
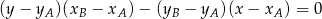
W naszej sytuacji
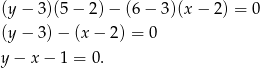
Zatem dla 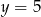 mamy
mamy 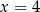 .
.
Odpowiedź: