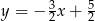Zadanie nr 8157792
Punkt 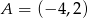 oraz
oraz 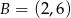 są symetryczne względem prostej
są symetryczne względem prostej 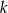 . Wyznacz równanie prostej
. Wyznacz równanie prostej 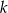 .
.
Rozwiązanie
Jeżeli wykonamy szkicowy rysunek to dostrzegamy, że szukana prosta to symetralna odcinka 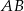 .
.
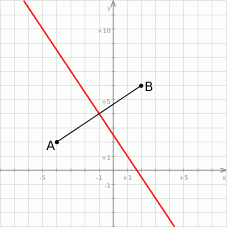
Sposób I
Najpierw wyznaczamy współczynnik kierunkowy prostej postaci: 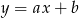 przechodzącej przez punkty
przechodzącej przez punkty 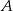 i
i 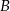
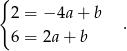
Odejmujemy stronami równania i otrzymujemy
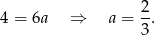
Symetralna odcinka 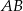 jest prostopadła do prostej przechodzącej przez punkty
jest prostopadła do prostej przechodzącej przez punkty 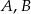 , więc musi być postaci
, więc musi być postaci 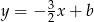 . Ponadto, prosta ta musi przechodzić przez środek
. Ponadto, prosta ta musi przechodzić przez środek 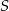 odcinka
odcinka 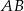 . Obliczamy współrzędne środka odcinka
. Obliczamy współrzędne środka odcinka 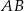
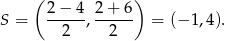
Podstawiamy współrzędne punktu 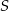 i obliczamy wyraz wolny
i obliczamy wyraz wolny 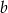
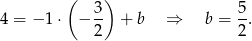
Zatem
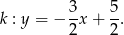
Sposób II
Symetralna odcinka 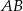 to zbiór punktów
to zbiór punktów 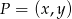 , które są równo odległe od punktów
, które są równo odległe od punktów 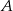 i
i 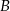 . Punkty te muszą więc spełniać równanie.
. Punkty te muszą więc spełniać równanie.
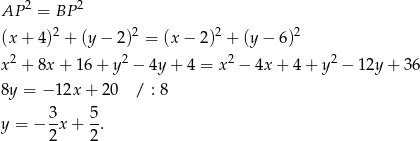
Odpowiedź: