Zadanie nr 8185465
W czworokącie 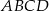 dane są
dane są ![−→ −→ AB = [6,− 3], DA = [− 8,− 7]](https://img.zadania.info/zad/8185465/HzadT1x.gif) oraz środek
oraz środek 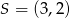 przekątnej
przekątnej 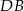 . Wyznacz współrzędne rzutu prostopadłego punktu
. Wyznacz współrzędne rzutu prostopadłego punktu 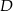 na prostą
na prostą 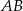 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
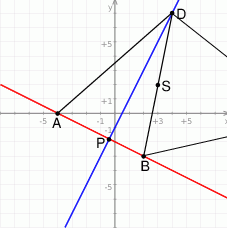
Powinno być jasne, że jeżeli są ustalone wektory 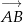 i
i 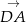 oraz środek odcinka
oraz środek odcinka 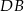 , to jednoznacznie da się wyliczyć współrzędne punktów
, to jednoznacznie da się wyliczyć współrzędne punktów 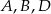 . Rzeczywiście, jeżeli oznaczymy
. Rzeczywiście, jeżeli oznaczymy 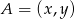 to mamy
to mamy
![−→ [6,− 3] = AB = [xB − x,yB − y] ⇒ B = (xB,yB ) = (x+ 6,y − 3) − → [− 8,− 7] = DA = [x− xD ,y − yD ] ⇒ D = (xD ,yD ) = (x+ 8,y+ 7).](https://img.zadania.info/zad/8185465/HzadR6x.gif)
Teraz wystarczy skorzystać z podanego środka odcinka 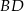 .
.
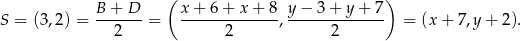
Zatem 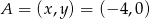 oraz
oraz 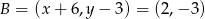 i
i 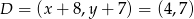 .
.
Zastanówmy się co dalej. Szukany rzut 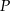 punktu
punktu 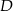 na prostą
na prostą 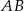 to punkt wspólny tej prostej oraz prostej prostopadłej do
to punkt wspólny tej prostej oraz prostej prostopadłej do 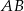 i przechodzącej przez
i przechodzącej przez 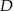 . Taki jest plan: napiszemy równania obu tych prostych i znajdziemy ich punkt wspólny
. Taki jest plan: napiszemy równania obu tych prostych i znajdziemy ich punkt wspólny 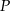 .
.
Równanie prostej 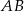 można wyznaczyć wprost z układu równań, można je też napisać używając wzoru na równanie prostej przechodzącej przez dwa punkty. My jednak, dla urozmaicenia, napiszemy je używając postaci parametrycznej. Wszystkie punkty prostej
można wyznaczyć wprost z układu równań, można je też napisać używając wzoru na równanie prostej przechodzącej przez dwa punkty. My jednak, dla urozmaicenia, napiszemy je używając postaci parametrycznej. Wszystkie punkty prostej 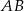 są postaci
są postaci
![−→ (x,y) = A + t⋅AB = (− 4,0) + t[6 ,−3 ] = (− 4 + 6t,− 3t), gdzie t ∈ R](https://img.zadania.info/zad/8185465/HzadR20x.gif)
Mamy więc
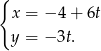
Równanie prostej prostopadłej do 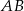 i przechodzącej przez punkt
i przechodzącej przez punkt 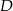 napiszemy korzystając ze wzoru
napiszemy korzystając ze wzoru
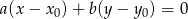
na równanie prostej prostopadłej do wektora ![→ v = [a,b]](https://img.zadania.info/zad/8185465/HzadR25x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 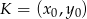 .
.
W naszej sytuacji mamy ![→ −→ v = AB = [6,− 3]](https://img.zadania.info/zad/8185465/HzadR27x.gif) oraz
oraz 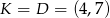 . Zatem równanie prostej
. Zatem równanie prostej 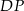 ma postać
ma postać
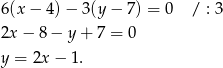
Pozostało znaleźć jej punkt wspólny z prostą 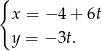 Podstawiamy wartości
Podstawiamy wartości  i
i 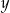 do równania i mamy
do równania i mamy
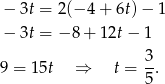
Daje to nam punkt
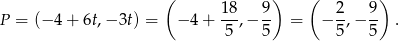
Odpowiedź: