Zadanie nr 8220984
Punkty 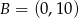 i
i 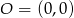 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 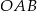 , w którym
, w którym 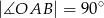 . Przyprostokątna
. Przyprostokątna 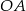 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 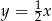 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 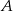 i długość przyprostokątnej
i długość przyprostokątnej 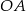 .
.
Rozwiązanie
Zaczynamy oczywiście od szkicowego rysunku.
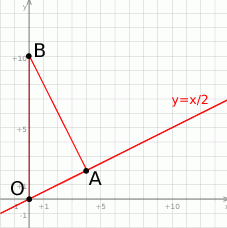
Dosyć łatwo jest napisać równanie prostej 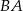 . Jest ona prostopadła do
. Jest ona prostopadła do 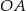 , więc jest postaci
, więc jest postaci 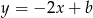 oraz przechodzi przez
oraz przechodzi przez 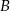 . Stąd
. Stąd 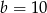 . Zatem ma ona równanie
. Zatem ma ona równanie 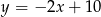 . Szukamy teraz punktu wspólnego tej prostej z prostą
. Szukamy teraz punktu wspólnego tej prostej z prostą 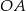 .
.
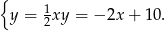
Odejmujemy od pierwszego równania drugie (albo porównujemy 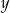 -ki) i mamy
-ki) i mamy
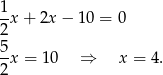
stąd 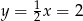 . Pozostało wyliczyć długość
. Pozostało wyliczyć długość 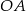
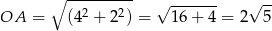
Odpowiedź: