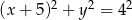Zadanie nr 8240220
Dane są punkty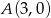 
i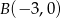 
. Wyznacz równanie krzywej, utworzonej przez wszystkie punkty płaszczyzny, których odległość od punktu 
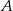jest 2 razy większa od odległości od punktu 
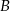. Jaką figurę opisuje ta krzywa?
Rozwiązanie
Załóżmy, że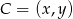 
jest punktem tej krzywej. Mamy wtedy
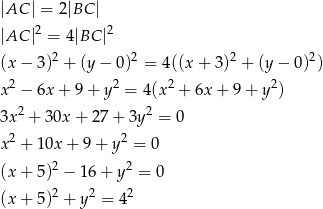
Szukana krzywa to okrąg o środku w punkcie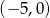 
i promieniu 4.
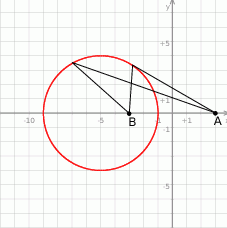
Dla ciekawskich, znaleziony okrąg to przykład tzw. okręgu Apoloniusza – można sobie wygooglać.
Odpowiedź: 
