/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8311157

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 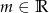m ∈ R , dla których równanie

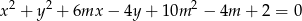
2 2 2 x + y + 6mx − 4y + 1 0m − 4m + 2 = 0

opisuje okrąg. Jaka jest największa możliwa długość tego okręgu?

Rozwiązanie

Przekształćmy dane równanie tak, aby było widać jaki jest środek i promień danego okręgu.

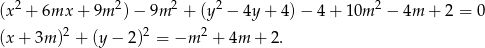
2 2 2 2 2 (x + 6mx + 9m )− 9m + (y − 4y + 4) − 4 + 10m − 4m + 2 = 0 (x+ 3m )2 + (y − 2 )2 = −m 2 + 4m + 2.

Jeżeli równanie to ma opisywać okrąg, to jego prawa strona musi być dodania (bo jest to kwadrat promienia), czyli

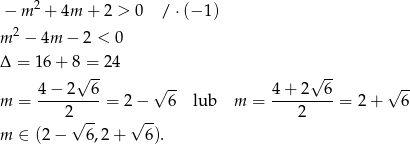
− m 2 + 4m + 2 > 0 / ⋅(− 1) 2 m − 4m − 2 < 0 Δ = 16+ 8 = 24 √ -- √ -- m = 4-−-2--6-= 2− √ 6- lub m = 4-+-2--6-= 2+ √ 6- 2 2 m ∈ (2− √ 6,2+ √ 6).

Największą długość okręgu otrzymamy, gdy najdłuższy będzie jego promień, czyli gdy największa będzie wartość funkcji

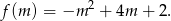
f (m) = −m 2 + 4m + 2.

Znamy już miejsca zerowe tej funkcji, więc łatwo wyznaczyć pierwszą współrzędną wierzchołka paraboli będącej jej wykresem – znajduje się on dokładnie w środku między pierwiastkami.

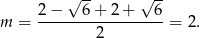
√ -- √ -- m = 2−---6-+-2-+---6-= 2. 2

Mamy wtedy 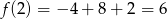f(2) = − 4 + 8 + 2 = 6 , więc promień okręgu jest wtedy równy 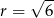√ -- r = 6 . Długość okręgu to

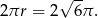
√ -- 2πr = 2 6π .

 
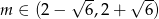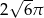Odpowiedź: m ∈ (2 − √ 6,2 + √ 6) , maksymalna długość: √ -- 2 6 π .

Wersja PDF