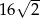Zadanie nr 8386114
Dany jest okrąg 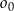 o równaniu
o równaniu 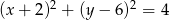 . W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi  styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 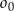 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 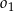 oraz
oraz 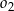 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
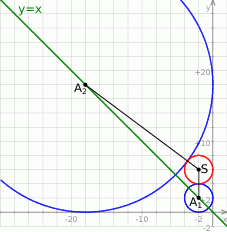
Zauważmy, że okrąg, który jest zawarty w II ćwiartce układu i jest styczny do obu osi układu musi mieć środek 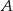 na prostej
na prostej 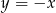 oraz promień równy wartości bezwzględnej współrzędnych środka. Szukamy więc okręgów postaci
oraz promień równy wartości bezwzględnej współrzędnych środka. Szukamy więc okręgów postaci
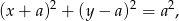
dla pewnego 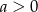 . Pozostało teraz zapisać informację o tym, że okrąg ten ma być styczny zewnętrznie do danego okręgu o środku
. Pozostało teraz zapisać informację o tym, że okrąg ten ma być styczny zewnętrznie do danego okręgu o środku 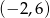 i promieniu 2. Dwa okręgi są styczne zewnętrznie, gdy odległość ich środków jest równa sumie ich promieni. Musimy więc rozwiązać równanie
i promieniu 2. Dwa okręgi są styczne zewnętrznie, gdy odległość ich środków jest równa sumie ich promieni. Musimy więc rozwiązać równanie
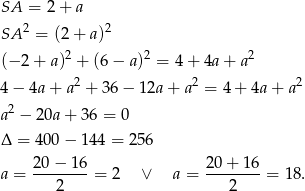
Środki okręgów 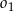 i
i 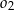 mają więc współrzędne
mają więc współrzędne 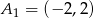 i
i 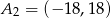 . Odległość tych punktów to
. Odległość tych punktów to
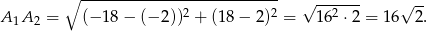
Odpowiedź: