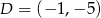Zadanie nr 8428712
Punkt 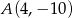 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 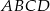 . Dwa boki równoległoboku zawierają się w prostych o równaniach
. Dwa boki równoległoboku zawierają się w prostych o równaniach 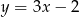 i
i 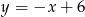 . Wyznacz pozostałe wierzchołki równoległoboku.
. Wyznacz pozostałe wierzchołki równoległoboku.
Rozwiązanie
Zacznijmy od schematycznego rysunku.
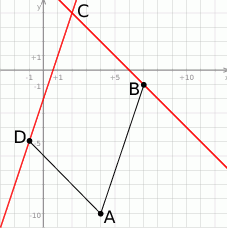
Od ręki możemy wyliczyć współrzędne punktu 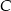 – wystarczy znaleźć punkt wspólny podanych prostych. Od razu porównujemy
– wystarczy znaleźć punkt wspólny podanych prostych. Od razu porównujemy 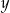 -ki.
-ki.
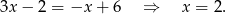
Stąd 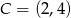 .
.
Aby wyznaczyć wpółrzędne pozostałych wierzchołków napiszemy równania prostych 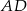 i
i 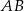 .
.
Prosta 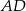 jest równoległa do prostej
jest równoległa do prostej 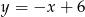 , jest zatem postaci
, jest zatem postaci 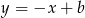 . Ponieważ przechodzi przez punkt
. Ponieważ przechodzi przez punkt  to
to
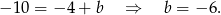
Podobnie, prosta 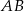 jest postaci
jest postaci 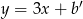 oraz
oraz

Szukamy punktu 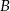 , czyli punktu wspólnego prostych
, czyli punktu wspólnego prostych 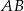 i
i 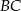 (porównujemy
(porównujemy 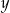 -ki).
-ki).
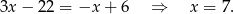
Zatem 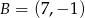 . Podobnie, przecinamy proste
. Podobnie, przecinamy proste 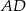 i
i 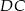 .
.
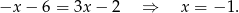
Zatem 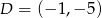 .
.
Odpowiedź: 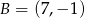 ,
, 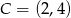 ,
,