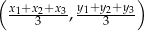/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8448802

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz współrzędne środka ciężkości trójkąta w zależności od współrzędnych jego wierzchołków.

Rozwiązanie

Oznaczmy współrzędne wierzchołków przez

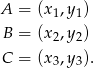
A = (x ,y ) 1 1 B = (x2,y2) C = (x ,y ). 3 3

PIC

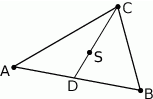
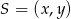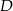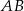To co musimy zrobić, to znaleźć współrzędne punktu S = (x,y) przecięcia się środkowych tego trójkąta. Środek D boku AB ma współrzędne

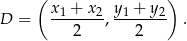
( ) D = x1-+-x2-, y1 +-y2 . 2 2

Punkt 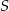S najłatwiej jest wyliczyć posługując się wektorami oraz faktem, że dzieli on środkową 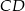CD w stosunku 2:1. Mamy zatem

−→ 2 −→ CS = -CD 3 [ ] [x − x ,y− y ] = 2- x1-+-x2-− x , y1 +-y2− y 3 3 3 2 3 2 3 [x + x 2 y + y 2 ] [x − x 3,y− y3] = -1----2-− --x3,-1----2-− -y3 . 3 3 3 3

Mamy stąd równania

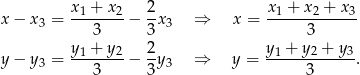
x + x 2 x + x + x x − x 3 = -1----2-− --x3 ⇒ x = -1----2----3- 3 3 3 y1-+-y2- 2- y1 +-y2 +-y3- y − y 3 = 3 − 3 y3 ⇒ y = 3 .

 
Odpowiedź: ( ) x1+x2+x3, y1+y-2+y-3 3 3

Wersja PDF