/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8458744

Dodaj do ulubionych
Dodaj do rozwiązanych

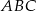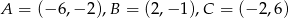Dany jest trójkąt ABC , gdzie A = (− 6,− 2),B = (2 ,−1 ),C = (− 2,6) .

  • Wyznacz równanie prostej zawierającej bok AC .
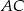  • Oblicz długość środkowej AD .
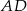  • Wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka C .
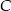  • Oblicz pole tego trójkąta.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

  • Szukamy prostej w postaci 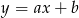y = ax + b i podstawiamy współrzędne punktów 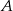A i C .
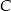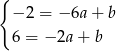
    { − 2 = −6a + b 6 = − 2a+ b

    Odejmujemy od drugiego równania pierwsze i mamy

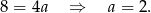
    8 = 4a ⇒ a = 2.

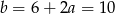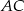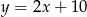    Stąd b = 6+ 2a = 10 i prosta AC ma równanie y = 2x+ 10 .  
    Odpowiedź: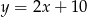 y = 2x + 10

  • Obliczamy najpierw współrzędne środka 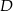D odcinka BC .
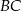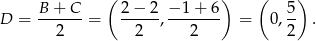
    ( ) ( ) B-+-C- 2-−-2- −-1+--6 5- D = 2 = 2 , 2 = 0,2 .

    Stąd

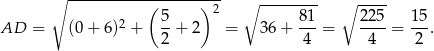
    ∘ -----------(------)-2 ∘ -------- ∘ ---- 2 5- 81- 225- 15- AD = (0 + 6) + 2 + 2 = 3 6+ 4 = 4 = 2 .

     
    Odpowiedź: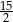 125

  • Wyznaczmy najpierw równanie prostej 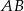AB – postępujemy dokładnie tak samo jak w przypadku prostej 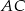AC : podstawiamy do wzoru 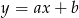y = ax + b współrzędne punktów 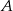A i B .
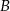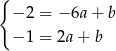
    { − 2 = −6a + b − 1 = 2a+ b

    Odejmujemy od drugiego równania pierwsze i mamy

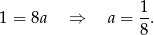
    1 1 = 8a ⇒ a = --. 8

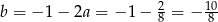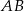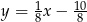    Stąd 2 10 b = − 1 − 2a = − 1 − 8 = − 8- i prosta AB ma równanie y = 18 x− 180 .

    Wysokość 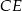CE jest prostopadła do prostej 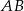AB , więc ma równanie postaci 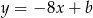y = − 8x+ b . Współczynnik 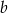b obliczamy podstawiając współrzędne punktu C .

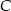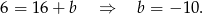
    6 = 16 + b ⇒ b = − 10.

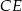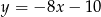    Wysokość CE ma więc równanie y = − 8x − 10 .  
    Odpowiedź: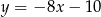 y = − 8x − 10

  • Pole trójkąta 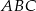ABC obliczymy na dwa sposoby.

    Sposób I

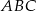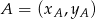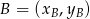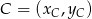    Aby obliczyć pole trójkąta ABC , korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA ,yA) , B = (xB ,yB) i C = (xC,yC ) .

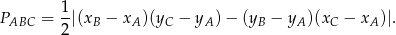
    P = 1|(x − x )(y − y )− (y − y )(x − x )|. ABC 2 B A C A B A C A

    W naszej sytuacji mamy

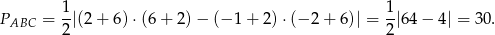
    1 1 PABC = --|(2 + 6) ⋅(6+ 2)− (− 1+ 2)⋅(− 2 + 6)| = --|6 4− 4| = 30. 2 2

    Sposób II

    Wyznaczmy najpierw spodek 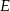E wysokości 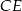CE , czyli punkt wspólny prostych 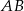AB i CE .

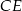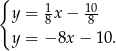
    { y = 18x − 108 y = − 8x− 10.

    Odejmujemy od pierwszego równania drugie i mamy

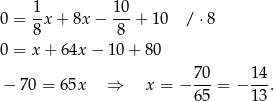
    1 10 0 = --x+ 8x − ---+ 10 / ⋅8 8 8 0 = x + 64x − 10+ 80 7 0 14 − 70 = 65x ⇒ x = − --- = − ---. 6 5 13

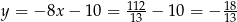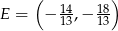    Stąd y = − 8x − 10 = 11123-− 10 = − 1183 i ( ) E = − 1143,− 1183 . Obliczamy teraz długość podstawy 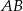AB i wysokości CE .

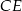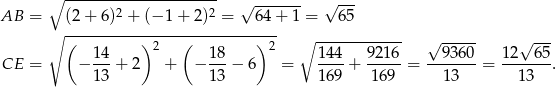
    ∘ --------------------- √ ------- √ --- AB = (2 + 6)2 + (− 1 + 2)2 = 64 + 1 = 65 ∘ (----------)----(---------)-- ∘ ------------ √ ----- √ --- 14 2 18 2 144 9216 9360 12 65 CE = − ---+ 2 + − ---− 6 = ----+ -----= -------= -------. 13 13 169 169 13 13

    Pole trójkąta 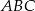ABC jest więc równe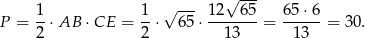

    --- √ --- P = 1-⋅AB ⋅CE = 1-⋅√ 65 ⋅ 12-65-= 65-⋅6-= 30. 2 2 13 13

     
    Odpowiedź: 30

Wersja PDF