/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8475641

Dodaj do ulubionych
Dodaj do rozwiązanych

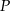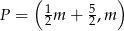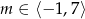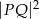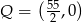W układzie współrzędnych rozważmy wszystkie punkty P postaci: ( ) P = 1m + 5,m 2 2 , gdzie m ∈ ⟨− 1,7⟩ . Oblicz najmniejszą i największą wartość 2 |PQ | , gdzie ( 55 ) Q = 2-,0 .

Rozwiązanie

Liczymy

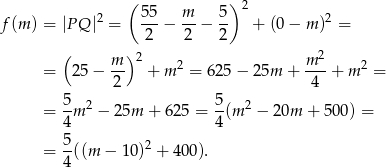
( ) 2 f(m ) = |PQ |2 = 55-− m- − 5- + (0 − m )2 = 2 2 2 ( m )2 m 2 = 25 − -- + m 2 = 625 − 25m + --- + m 2 = 2 4 5- 2 5- 2 = 4m − 25m + 625 = 4(m − 20m + 500) = 5 2 = -((m − 10) + 400 ). 4

Widać teraz, że wierzchołek paraboli będącej wykresem tej funkcji znajduje się na prawo od przedziału 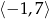⟨− 1,7⟩ , więc funkcja jest na tym przedziale malejąca (bo ramiona są skierowane w górę). Zatem jej największa wartość to

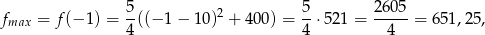
fmax = f (− 1) = 5((− 1 − 10 )2 + 40 0) = 5-⋅521 = 2605-= 651,25 , 4 4 4

a wartość najmniejsza to

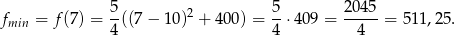
5- 2 5- 2045- fmin = f(7 ) = 4((7 − 10) + 400 ) = 4 ⋅409 = 4 = 511,25.

 
Odpowiedź: 2045 2605 fmin = --4- = 51 1,25, fmax = -4--= 651,2 5

Wersja PDF