/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8506371

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątna 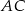AC czworokąta 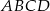ABCD zawiera się w prostej o równaniu 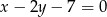x − 2y − 7 = 0 . Wierzchołki 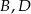B,D tego czworokąta mają współrzędne 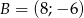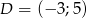B = (8;− 6) , D = (− 3;5 ) . Oblicz współrzędne punktu przecięcia się przekątnych czworokąta ABCD .

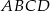Rozwiązanie

Rozpoczynamy od szkicowego rysunku

PIC

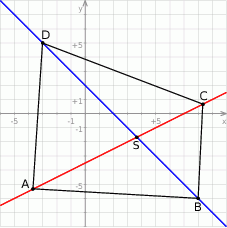
Napiszmy równanie prostej 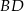BD – szukamy prostej w postaci 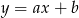y = ax+ b i podstawiamy współrzędne punktów 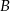B i D .

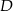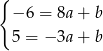
{ − 6 = 8a + b 5 = − 3a + b

Odejmujemy od pierwszego równania drugie (żeby skrócić 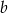b ) i mamy

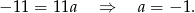
−1 1 = 11a ⇒ a = − 1.

Stąd 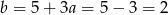b = 5 + 3a = 5− 3 = 2 i prosta 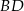BD ma równanie 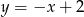y = −x + 2 . Pozostało wyznaczyć jej punkt wspólny 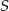S z podaną prostą AC .

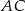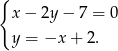
{ x− 2y− 7 = 0 y = −x + 2.

Podstawiamy 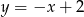y = −x + 2 z drugiego równania do pierwszego i mamy

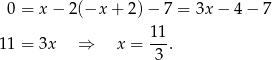
0 = x − 2(−x + 2) − 7 = 3x − 4 − 7 11- 1 1 = 3x ⇒ x = 3 .

Stąd

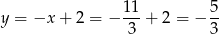
y = −x + 2 = − 11-+ 2 = − 5- 3 3

i 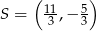( ) S = 113 ,− 53 .  
Odpowiedź: (11 5) -3 ,− 3

Wersja PDF