/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8508909

Dodaj do ulubionych
Dodaj do rozwiązanych

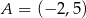Punkt A = (− 2,5) jest jednym z wierzchołków trójkąta równoramiennego 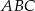ABC , w którym 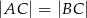|AC | = |BC | . Pole tego trójkąta jest równe 15. Bok 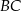BC jest zawarty w prostej o równaniu 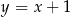y = x+ 1 . Oblicz współrzędne wierzchołka C .

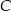Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

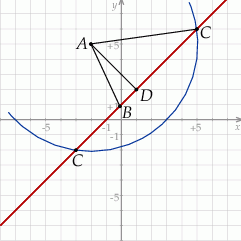
Plan jest następujący: obliczymy długość wysokości opuszczonej na bok 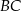BC , co dzięki podanemu polu pozwoli nam wyliczyć długość ramienia 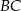BC trójkąta. Znając długość ramienia 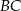BC znajdziemy punkt 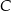C jako punkt wspólny okręgu o środku w punkcie 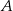A i promieniu 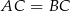AC = BC oraz podanej prostej y = x + 1 .

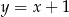Długość wysokości 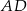AD to odległość punktu 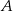A od prostej 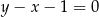y− x− 1 = 0 , czyli

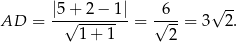
|5-+-2-−-1|- -6-- √ -- AD = √ 1 + 1 = √ 2 = 3 2.

Ponieważ pole jest równe 15 mamy

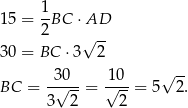
1- 15 = 2BC ⋅AD √ -- 30 = BC ⋅3 2 --30- -10- √ -- BC = √ --= √ --= 5 2. 3 2 2

To oznacza, że punkt 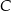C leży na okręgu o środku w punkcie 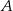A i promieniu 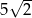√ -- 5 2 . Okrąg ten ma równanie

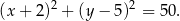
2 2 (x + 2) + (y − 5) = 50.

Szukamy jego punktów wspólnych z podaną prostą – podstawiamy 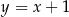y = x+ 1 .

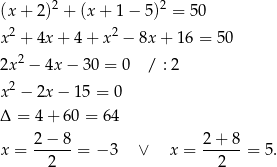
(x + 2)2 + (x+ 1− 5)2 = 50 2 2 x + 4x + 4 + x − 8x + 16 = 50 2x2 − 4x − 30 = 0 / : 2 2 x − 2x − 15 = 0 Δ = 4+ 60 = 64 x = 2−-8-= − 3 ∨ x = 2+--8-= 5. 2 2

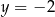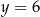Mamy wtedy y = − 2 i y = 6 odpowiednio. Zatem 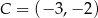C = (− 3,− 2) lub C = (5,6) .  
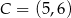Odpowiedź: 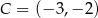C = (− 3,− 2) lub C = (5,6)

Wersja PDF