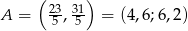/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8532696

Dodaj do ulubionych
Dodaj do rozwiązanych

Okrąg o środku w punkcie 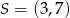S = (3,7) jest styczny do prostej o równaniu 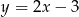y = 2x− 3 . Oblicz współrzędne punktu styczności.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

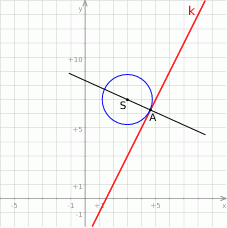
Zauważmy, że jeżeli 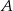A jest szukanym punktem styczności, to dana prosta

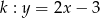
k : y = 2x − 3

i prosta 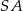SA są prostopadłe. To pozwala dość łatwo napisać równanie prostej 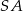SA . Ma być ona prostopadła do 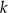k , czyli musi być postaci 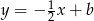y = − 1x + b 2 . Współczynnik 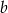b obliczamy podstawiając współrzędne punktu S .

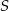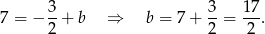
3 3 17 7 = − --+ b ⇒ b = 7 + --= ---. 2 2 2

Pozostało teraz wyznaczyć punkt wspólny 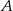A prostych 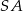SA i k .

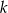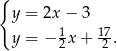
{ y = 2x − 3 y = − 12x + 172 .

Odejmujemy od pierwszego równania drugie i mamy

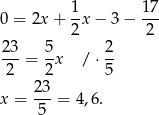
1- 1-7 0 = 2x + 2x − 3 − 2 23 5 2 ---= --x / ⋅-- 2 2 5 x = 23-= 4 ,6 . 5

Zatem

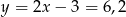
y = 2x − 3 = 6,2

i 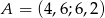A = (4,6;6,2)  
Odpowiedź: ( ) A = 23, 31 = (4 ,6;6,2) 5 5

Wersja PDF