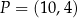Zadanie nr 8663007
W układzie współrzędnych na płaszczyźnie dane są punkty: 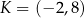 i
i 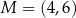 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 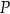 takiego, że jeden z trzech punktów
takiego, że jeden z trzech punktów 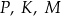 jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
Rozwiązanie
Jeżeli spróbujemy sobie wyobrazić opisaną sytuację, to łatwo zauważyć że są trzy różne konfiguracje.
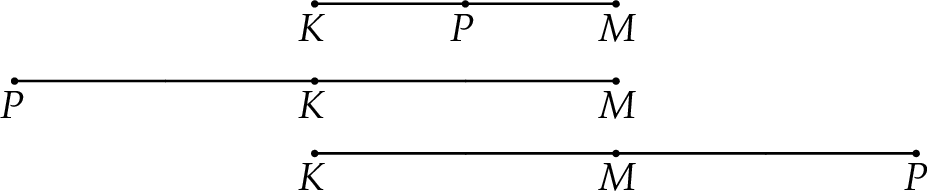
Punkt 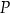 może być po prostu środkiem odcinka
może być po prostu środkiem odcinka 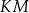 . Wtedy
. Wtedy
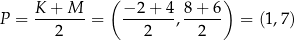
Druga możliwa sytuacja to taka, że punkt 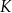 jest środkiem odcinka
jest środkiem odcinka 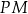 . Wtedy
. Wtedy
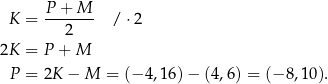
Ostatnia możliwość jest taka, że punkt 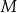 jest środkiem odcinka
jest środkiem odcinka 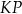 . Wtedy
. Wtedy
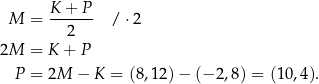
Odpowiedź: 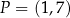 lub
lub 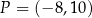 lub
lub