/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8718257

Dodaj do ulubionych
Dodaj do rozwiązanych

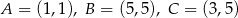Punkty A = (1,1), B = (5,5), C = (3,5) są wierzchołkami trapezu równoramiennego 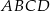ABCD niebędącego równoległobokiem, w którym AB ∥ CD .

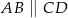  • Wyznacz równanie osi symetrii tego trapezu.
  • Oblicz pole tego trapezu.

Rozwiązanie

Rozpoczynamy od naszkicowania opisanej sytuacji.

PIC

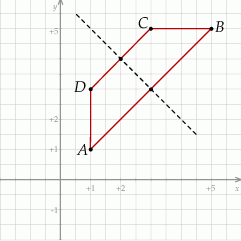
  • Osią symetrii trapezu 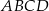ABCD jest prosta prostopadła do podstaw i przechodząca przez ich środki. Łatwo wyliczyć środek podstawy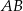 AB
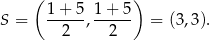
    ( ) 1+-5--1-+-5- S = 2 , 2 = (3,3).

    Szukamy zatem prostej prostopadłej do 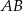AB i przechodzącej przez 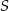S . Zrobimy to na dwa sposoby.

    Sposób I

    Łatwo zauważyć (lub wyliczyć ze wzoru na równanie prostej przechodzącej przez dwa punkty), że prosta 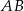AB ma równanie 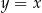y = x . Zatem prosta prostopadła do 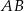AB będzie miała równanie postaci 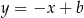y = −x + b . Współczynnik 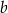b wyznaczamy podstawiając współrzędne punktu S .

    3 = − 3 + b ⇒ b = 6.

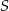    Zatem szukana oś symetrii ma równanie y = −x + 6 .

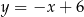    Sposób II

    Tym razem skorzystamy ze wzoru

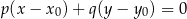
    p(x − x0) + q(y − y0) = 0

    na równanie prostej prostopadłej do wektora →v = [p,q] i przechodzącej przez punkt (x0,y0) .

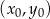    W naszej sytuacji mamy

    → → v = AB = [5− 1,5− 1] = [4,4]

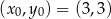    oraz (x 0,y0) = (3,3) . Zatem szukana prosta ma równanie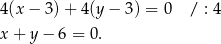

    4(x − 3)+ 4 (y− 3) = 0 / : 4 x + y − 6 = 0.

     
    Odpowiedź: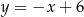 y = −x + 6

  • Wysokość trapezu jest równa odległości punktu 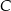C od prostej 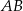AB , która jak już zauważyliśmy ma równanie 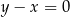y − x = 0 . Korzystając ze wzoru na odległość punktu od prostej mamy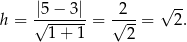
    -|5-−-3|- -2-- √ -- h = √ 1-+-1-= √ 2-= 2.

    Łatwo też wyliczyć długość podstawy AB

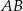
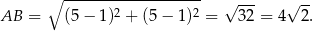
    ∘ ------------------- √ --- √ -- AB = (5− 1)2 + (5− 1)2 = 32 = 4 2 .

    Odrobinę trudniej jest z podstawą 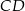CD , bo wciąż nie znamy współrzędnych wierzchołka 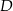D . Spróbujemy to teraz zrobić.

    Prosta 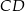CD jest równoległa do 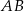AB , czyli jest postaci 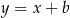y = x + b . Współczynnik 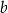b wyznaczamy podstawiając współrzędne punktu C .

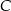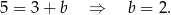
    5 = 3 + b ⇒ b = 2.

    Znajdźmy teraz jej punkt wspólny z wyznaczoną wcześniej osią symetrii trapezu, czyli środek odcinka CD .

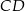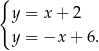
    { y = x+ 2 y = −x + 6.

    Dodając równania stronami mamy

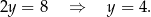
    2y = 8 ⇒ y = 4.

    Zatem 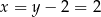x = y − 2 = 2 i środek odcinka 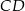CD ma współrzędne 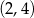(2,4) . Łatwo teraz wyznaczyć współrzędne punktu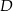 D

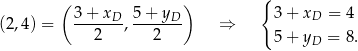
    ( ) { 3-+-xD- 5-+-yD- 3 + xD = 4 (2,4) = 2 , 2 ⇒ 5 + y = 8. D

    Stąd 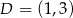D = (1,3) oraz

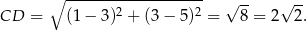
    ∘ ------------------- 2 2 √ -- √ -- CD = (1 − 3 ) + (3 − 5) = 8 = 2 2.

    Pole trapezu jest więc równe

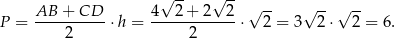
    √ -- √ -- P = AB--+-CD--⋅ h = 4--2-+-2---2⋅ √ 2 = 3√ 2-⋅√ 2-= 6. 2 2

     
    Odpowiedź: 6

Wersja PDF