Zadanie nr 8726572
W trójkącie prostokątnym 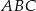 , gdzie
, gdzie 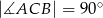 , wierzchołek
, wierzchołek 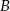 ma współrzędne
ma współrzędne 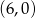 . Prosta
. Prosta 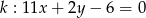 , zawierająca środkową trójkąta poprowadzoną z wierzchołka
, zawierająca środkową trójkąta poprowadzoną z wierzchołka 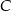 , przecina bok
, przecina bok 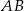 trójkąta w punkcie
trójkąta w punkcie 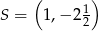 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 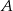 i
i 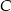 .
.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
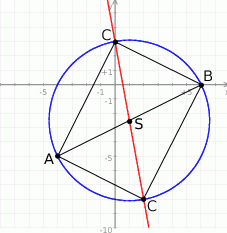
Ponieważ znamy współrzędne punktu 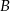 i środka
i środka 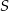 odcinka
odcinka 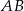 , możemy łatwo wyliczyć współrzędne punktu
, możemy łatwo wyliczyć współrzędne punktu 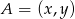 .
.
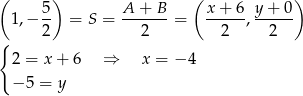
Zatem 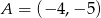 i pozostało wyznaczyć współrzędne punktu
i pozostało wyznaczyć współrzędne punktu 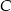 .
.
Sposób I
Ponieważ punkt 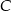 ma leżeć na prostej
ma leżeć na prostej 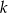 jest on postaci
jest on postaci 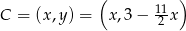 . Na mocy twierdzenia Pitagorasa mamy zatem
. Na mocy twierdzenia Pitagorasa mamy zatem
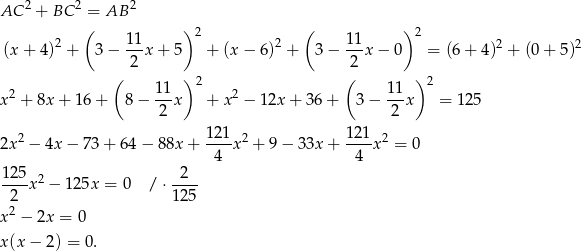
Zatem 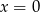 lub
lub 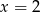 . Wtedy odpowiednio
. Wtedy odpowiednio 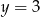 lub
lub 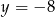 .
.
Sposób II
Ponieważ punkt 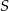 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 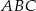 (zawsze środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej), więc wystarczy znaleźć punkty danej prostej
(zawsze środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej), więc wystarczy znaleźć punkty danej prostej 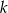 i okręgu o środku w punkcie
i okręgu o środku w punkcie 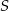 i promieniu
i promieniu 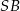 , gdzie
, gdzie
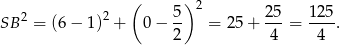
Podstawiamy więc do równania okręgu
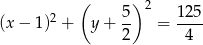
wyliczony z równania prostej 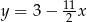 .
.
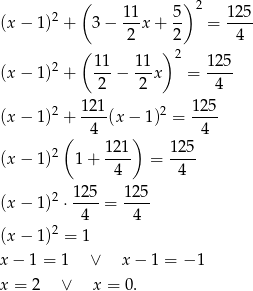
Jak poprzednio, otrzymujemy stąd 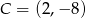 lub
lub 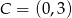 .
.
Odpowiedź: 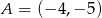 ,
, 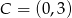 lub
lub