Zadanie nr 8729993
Wierzchołki trapezu 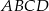 mają współrzędne:
mają współrzędne: 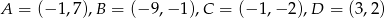 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 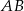 tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu
tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu 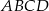 .
.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
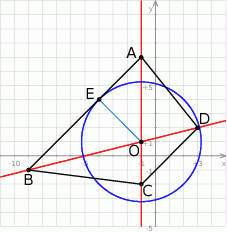
Aby znaleźć punkt 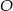 wspólny dla przekątnych
wspólny dla przekątnych 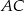 i
i 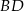 musimy wyznaczyć ich równania.
musimy wyznaczyć ich równania.
Równanie prostej 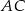 łatwo zgadnąć patrząc na współrzędne punktów
łatwo zgadnąć patrząc na współrzędne punktów 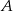 i
i 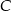 : jest to prosta
: jest to prosta 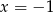 .
.
Szukamy teraz prostej 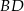 w postaci
w postaci 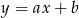 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 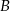 i
i 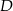 i mamy
i mamy
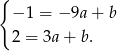
Odejmujemy od drugiego równania pierwsze i mamy 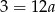 , czyli
, czyli 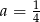 . Stąd
. Stąd 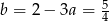 i prosta
i prosta 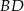 ma równanie:
ma równanie: 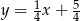 .
.
Wyznaczamy teraz punkt wspólny 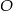 prostych
prostych 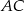 i
i 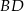 .
.
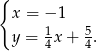
Podstawiając 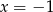 do drugiego równania mamy
do drugiego równania mamy 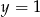 , więc
, więc 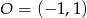 .
.
Do wyznaczenia promienia okręgu będziemy potrzebować równania prostej 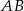 . Jak zwykle szukamy prostej w postaci
. Jak zwykle szukamy prostej w postaci 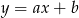 . Podstawimy współrzędne punktów
. Podstawimy współrzędne punktów 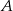 i
i 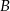 .
.
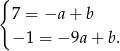
Odejmujemy od pierwszego równania drugie i mamy 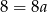 , czyli
, czyli 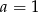 . Stąd
. Stąd 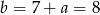 i prosta
i prosta 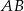 ma równanie:
ma równanie: 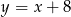 .
.
Dalszą część rozwiązania poprowadzimy na dwa sposoby.
Sposób I
Niech 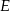 będzie punktem wspólnym szukanego okręgu i prostej
będzie punktem wspólnym szukanego okręgu i prostej 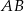 . Dość łatwo jest wyznaczyć równanie prostej
. Dość łatwo jest wyznaczyć równanie prostej 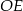 – jest to prosta prostopadła do
– jest to prosta prostopadła do 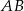 , czyli prosta postaci
, czyli prosta postaci 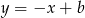 i przechodząca przez
i przechodząca przez 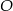 . Podstawiając współrzędne punktu
. Podstawiając współrzędne punktu 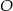 mamy
mamy
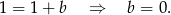
Jest to więc prosta: 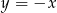 . Obliczamy teraz współrzędne punktu
. Obliczamy teraz współrzędne punktu 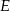 (czyli punktu wspólnego prostych
(czyli punktu wspólnego prostych 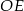 i
i 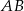 ).
).
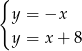
Odejmujemy od drugiego równania pierwsze i mamy 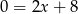 , czyli
, czyli 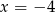 . Stąd
. Stąd 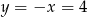 i
i 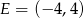 .
.
Obliczamy teraz długość promienia 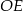 okręgu.
okręgu.
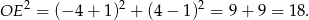
Szukany okrąg ma więc równanie
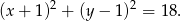
Sposób II
Długość promienia 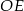 możemy obliczyć korzystając ze wzoru na odległość punktu
możemy obliczyć korzystając ze wzoru na odległość punktu 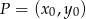 od prostej
od prostej 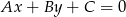 :
:
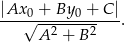
W naszej sytuacji 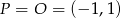 , a prosta to
, a prosta to 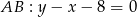 . Mamy zatem
. Mamy zatem
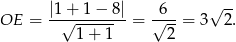
Szukany okrąg ma więc równanie
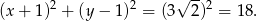
Odpowiedź: