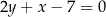Zadanie nr 8816846
Dane są równania prostych 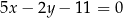 i
i 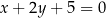 , w których zawierają się dwa boki równoległoboku. Punkt
, w których zawierają się dwa boki równoległoboku. Punkt 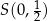 jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
Rozwiązanie
Znajdując punkt wspólny podanych prostych wyznaczymy jeden z wierzchołków równoległoboku. Podstawiamy z drugiego równania 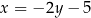 do pierwszego.
do pierwszego.
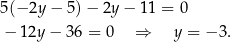
Zatem 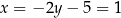 . Oznaczmy ten punkt przez
. Oznaczmy ten punkt przez 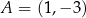 . Teraz możemy sobie naszkicować całą sytuację.
. Teraz możemy sobie naszkicować całą sytuację.
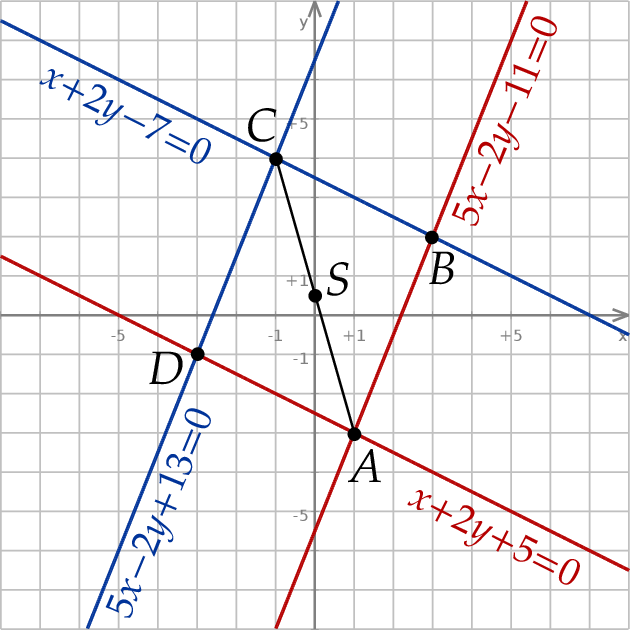
Mając dany punkt 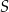 , łatwo wyznaczyć wierzchołek
, łatwo wyznaczyć wierzchołek 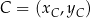 :
:
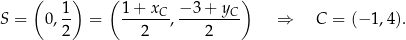
Teraz wystarczy napisać równania prostych równoległych do danych i przechodzących przez punkt 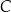 . Szukamy prostych postaci
. Szukamy prostych postaci 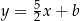 i
i 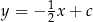 . Współczynniki
. Współczynniki 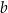 i
i  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 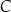 .
.
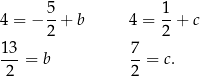
Zatem szukane proste to
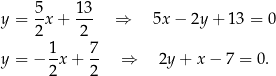
Odpowiedź: 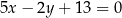 i
i