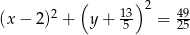/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8905185

Dodaj do ulubionych
Dodaj do rozwiązanych

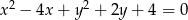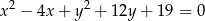Wyznacz równanie okręgu o promieniu 7 5 , który przechodzi przez punkty wspólne okręgów o równaniach x 2 − 4x + y2 + 2y + 4 = 0 i x 2 − 4x + y 2 + 1 2y+ 19 = 0 .

Rozwiązanie

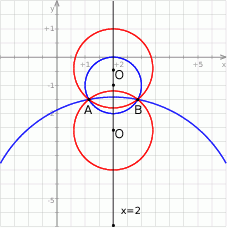
Aby wykonać szkicowy rysunek opisanej sytuacji, przekształćmy równania okręgów tak, aby było widać jakie mają środki i promienie.

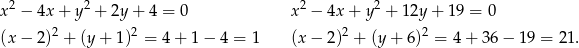
2 2 2 2 x − 4x + y + 2y + 4 = 0 x − 4x+ y + 12y + 19 = 0 (x − 2)2 + (y+ 1)2 = 4 + 1− 4 = 1 (x − 2)2 + (y + 6 )2 = 4+ 36− 19 = 21.

Możemy teraz wykonać szkicowy rysunek.

PIC

Wyznaczmy współrzędne punktów wspólnych 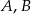A,B danych okręgów.

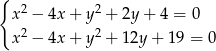
{ x2 − 4x + y2 + 2y + 4 = 0 x2 − 4x + y2 + 12y + 19 = 0

Odejmujemy od drugiego równania pierwsze i mamy

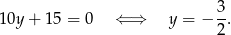
3 10y + 1 5 = 0 ⇐ ⇒ y = − -. 2

Podstawiamy tę wartość do przekształconego równania pierwszego okręgu.

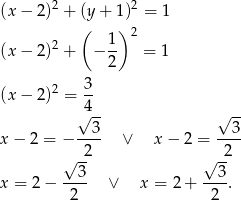
2 2 (x − 2 ) + ((y + 1)) = 1 2 1 2 (x − 2 ) + − -- = 1 2 2 3- (x − 2 ) = 4 √ 3- √ 3- x − 2 = − ---- ∨ x − 2 = ---- √ -2 √ -2 3 3 x = 2− ---- ∨ x = 2 + ----. 2 2

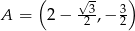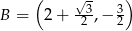Zatem ( √- ) A = 2 − -3,− 3 2 2 i ( √- ) B = 2+ -3-,− 3 2 2 .

Zauważmy teraz, że środek 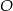O szukanego okręgu musi leżeć na symetralnej odcinka 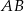AB , czyli na pionowej prostej

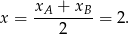
x = xA-+-xB- = 2. 2

W takim razie punkt 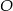O musi mieć współrzędne postaci 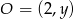O = (2,y) . Pozostało teraz wykorzystać informację o promieniu szukanego okręgu.

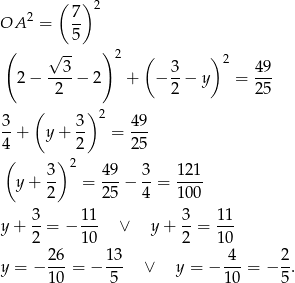
( ) 2 7 2 OA = -- ( --5 ) √ 3 2 ( 3 ) 2 49 2 − ----− 2 + − --− y = --- 2 2 25 ( )2 3-+ y + 3- = 49- 4 2 25 ( )2 y + 3- = 49-− 3-= 121- 2 25 4 100 3 11 3 1 1 y+ --= − --- ∨ y + --= --- 2 10 2 1 0 y = − 26- = − 13- ∨ y = − -4-= − 2-. 10 5 10 5

Są więc dwa okręgi spełniające warunki zadania:

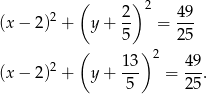
( ) 2 (x− 2)2 + y + 2- = 49- 5 25 ( ) 2 (x− 2)2 + y + 13- = 49-. 5 25

 
Odpowiedź: 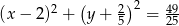2 ( 2) 2 49 (x − 2) + y + 5 = 25 lub ( ) 2 13 2 49- (x − 2) + y+ 5 = 25

Wersja PDF