/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 8957958

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że trójkąt 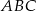ABC o wierzchołkach 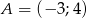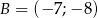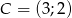A = (− 3;4) , B = (− 7;− 8) , C = (3;2) jest prostokątny.

Rozwiązanie

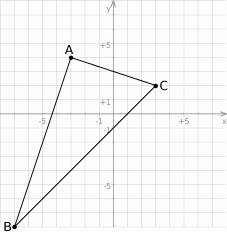
Jeżeli narysujemy podane punkty, to jest jasne, że kąt prosty powinien być przy wierzchołku 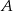A .

PIC

Sposób I

Aby sprawdzić czy tak jest w istocie, musimy sprawdzić czy 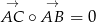→ → AC ∘AB = 0 . Liczymy

→ → AC ∘ AB = [3+ 3,2− 4]∘ [−7 + 3 ,− 8 − 4] = = [6,− 2]∘ [−4 ,−1 2] = − 24+ 24 = 0.

A więc istotnie trójkąt 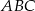ABC jest prostokątny.

Sposób II

Jeżeli nie chcemy korzystać z iloczynu skalarnego, korzystamy z twierdzenia odwrotnego do twierdzenia Pitagorasa.

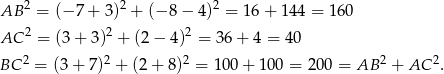
2 2 2 AB = (− 7 + 3) + (− 8− 4) = 16 + 144 = 160 2 2 2 AC = (3 + 3) + (2 − 4) = 36 + 4 = 40 BC 2 = (3+ 7)2 + (2+ 8)2 = 100 + 100 = 200 = AB 2 + AC 2.

Zatem istotnie 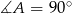∘ ∡A = 90 .

Wersja PDF