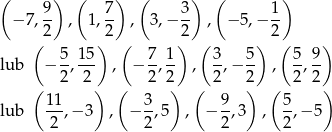Zadanie nr 9125511
Punkty 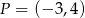 ,
, 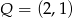 i
i 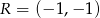 są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
Rozwiązanie
Zauważmy, że dwa z podanych punktów leżą na równoległych bokach równoległoboku. Nie wiemy jednak, które dwa punkty mają tę własność, więc rozważymy 3 przypadki.
Załóżmy najpierw, że 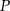 i
i 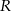 leżą na równoległych bokach równoległoboku
leżą na równoległych bokach równoległoboku 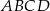 – możemy tak oznaczyć wierzchołki równoległoboku, aby
– możemy tak oznaczyć wierzchołki równoległoboku, aby 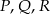 było odpowiednio środkami boków
było odpowiednio środkami boków  .
.
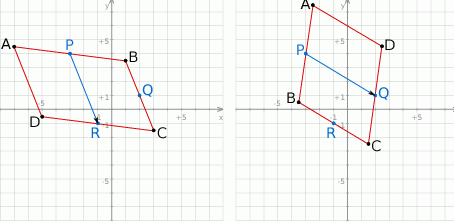
Zauważmy, że przy tych oznaczeniach
![−→ −→ −→ AD = BC = P R = [− 1 + 3,− 1 − 4] = [2,− 5].](https://img.zadania.info/zad/9125511/HzadR6x.gif)
To pozwala łatwo wyznaczyć współrzędne wierzchołków  i
i 
![[ ] ( ) 1-−→ 5- 3- C = Q + 2 BC = (2,1) + 1 ,− 2 = 3,− 2 [ ] ( ) 1-−→ 1-−→ 5- 7- Q = B + 2BC ⇒ B = Q − 2 BC = (2,1) − 1,− 2 = 1,2 .](https://img.zadania.info/zad/9125511/HzadR9x.gif)
Współrzędne punktów 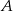 i
i 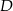 wyznaczamy z tego, że
wyznaczamy z tego, że 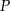 i
i 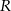 są środkami odcinków
są środkami odcinków 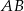 i
i 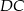 .
.
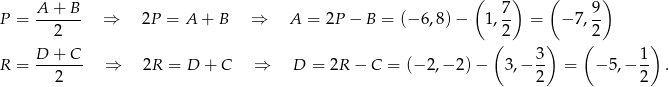
Załóżmy teraz, że 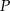 i
i 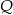 leżą na bokach równoległych – przyjmijmy, że
leżą na bokach równoległych – przyjmijmy, że 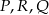 leżą odpowiednio na bokach
leżą odpowiednio na bokach 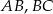 i
i 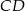 . Analogicznie jak poprzednio mamy
. Analogicznie jak poprzednio mamy
![−→ −→ −→ AD = BC = PQ = [2 + 3,1 − 4] = [5,− 3].](https://img.zadania.info/zad/9125511/HzadR22x.gif)
Obliczamy współrzędne wierzchołków 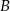 i
i 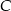 .
.
![[ ] ( ) 1−→ 5- 3- 3- 5- C = R + 2BC = (−1 ,−1 )+ 2,− 2 = 2,− 2 [ ] ( ) R = B + 1−B→C ⇒ B = R − 1−B→C = (− 1,− 1) − 5,− 3- = − 7, 1 . 2 2 2 2 2 2](https://img.zadania.info/zad/9125511/HzadR25x.gif)
Wyznaczamy teraz współrzędne wierzchołków 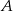 i
i 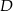
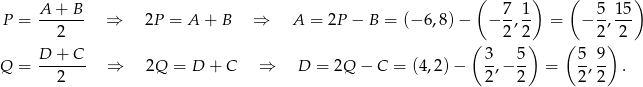
Pozostała ostatnia możliwość, gdy punkty 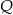 i
i 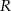 leżą na bokach równoległych. Załóżmy,
leżą na bokach równoległych. Załóżmy, 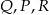 leżą odpowiednio na bokach
leżą odpowiednio na bokach 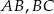 i
i 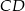 .
.
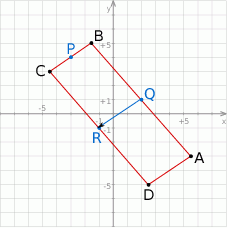
Mamy zatem
![−→ −→ −→ AD = BC = QR = [− 1 − 2,− 1 − 1] = [− 3,− 2].](https://img.zadania.info/zad/9125511/HzadR35x.gif)
Obliczamy współrzędne wierzchołków 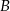 i
i 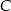 .
.
![[ ] ( ) 1-−→ 3- 9- C = P + 2 BC = (− 3,4) + − 2 ,−1 = − 2,3 [ ] ( ) 1-−→ 1-−→ 3- 3- P = B + 2 BC ⇒ B = P − 2BC = (− 3,4)− − 2,− 1 = − 2,5 .](https://img.zadania.info/zad/9125511/HzadR38x.gif)
Wyznaczamy teraz współrzędne wierzchołków 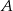 i
i 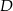
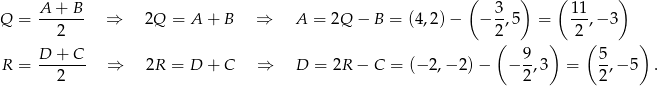
Odpowiedź: