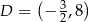Zadanie nr 9180291
Przekątna 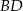 deltoidu zawiera się w prostej o równaniu
deltoidu zawiera się w prostej o równaniu 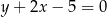 i ma taką samą długość jak przekątna
i ma taką samą długość jak przekątna 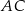 . Przekątne te przecinają się w punkcie
. Przekątne te przecinają się w punkcie 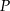 , takim że
, takim że 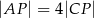 . Wierzchołek
. Wierzchołek 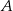 ma współrzędne
ma współrzędne 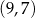 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków  i
i  tego deltoidu.
tego deltoidu.
Rozwiązanie
Szkicujemy deltoid.
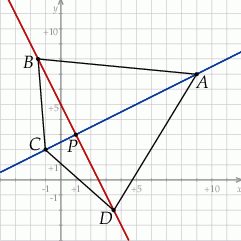
Podane informacje pozwalają łatwo napisać równanie przekątnej 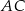 – jest to prosta prostopadła do
– jest to prosta prostopadła do 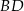 (bo przekątne deltoidu są prostopadłe), więc ma równanie postaci
(bo przekątne deltoidu są prostopadłe), więc ma równanie postaci 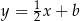 oraz przechodzi przez punkt
oraz przechodzi przez punkt 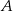 .
.
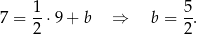
Przekątna 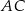 ma więc równanie
ma więc równanie 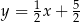 . Szukamy teraz jej punktu wspólnego
. Szukamy teraz jej punktu wspólnego 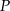 z przekątną
z przekątną 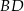 .
.
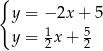
Odejmujemy od pierwszego równania drugie i mamy
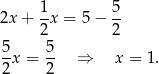
Stąd 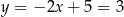 i
i 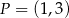 . Teraz wyznaczymy wierzchołek
. Teraz wyznaczymy wierzchołek 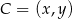 . Wiemy, że
. Wiemy, że
![−→ 1 −→ P C = -AP 4 [x− 1,y− 3] = 1[1 − 9,3 − 7] = [− 2,− 1]. 4](https://img.zadania.info/zad/9180291/HzadR15x.gif)
Stąd 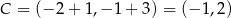 . Wiemy ponadto, że
. Wiemy ponadto, że
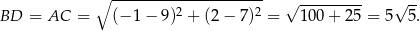
Aby wyznaczyć współrzędne punktów  i
i 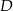 szukamy takich punktów
szukamy takich punktów 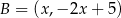 prostej
prostej 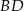 , dla których
, dla których
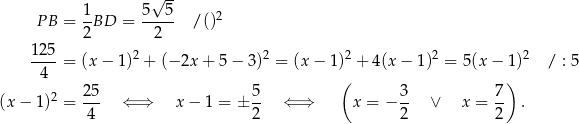
Mamy wtedy 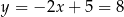 i
i 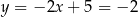 odpowiednio. Zatem
odpowiednio. Zatem 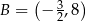 i
i 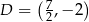 lub odwrotnie.
lub odwrotnie.
Odpowiedź: 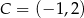 ,
, 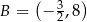 ,
, 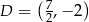 lub
lub 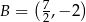 ,
,