Zadanie nr 9183390
W kwadracie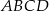 
dane są wierzchołek 
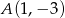i równanie prostej 
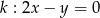w której zawiera się jedna z przekątnych kwadratu. Znajdź współrzędne wierzchołka 
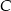oraz oblicz pole tego kwadratu.
Rozwiązanie
Wstawiając do wzoru sprawdzamy, że podana przekątna to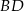 
(punkt 
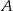na niej nie leży). Naszkicujmy sobie tę sytuację.
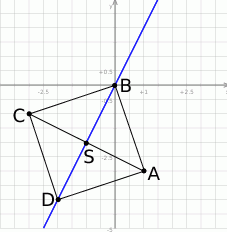
Gdy popatrzymy sobie na obrazek, to powinno być widać, że dość łatwo jest wyznaczyć wierzchołek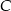 
– wystarczy napisać równanie prostej prostopadłej do 
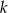i przechodzącej przez 
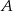(druga przekątna). Jej punkt wspólny 
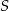z przekątną 
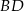ma być środkiem odcinka 
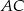, co pozwoli łatwo wyznaczyć punkt 
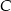. Gdybyśmy chcieli dodatkowo wyliczyć wierzchołki 
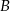i 
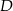(ale nie musimy tego robić), to wystarczy znaleźć punkty wspólne przekątnej 
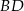i okręgu o środku 
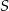i promieniu 
.
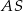Wszystko wiemy, to liczymy. Prosta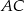 
ma postać 
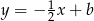(ma być prostopadła do 
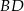). Współczynnik 
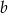wyliczamy podstawiając punkt 
.
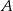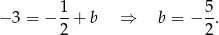
Szukamy jej punktu wspólnego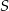 
z prostą 
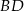(wstawiamy 
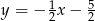) do równania prostej 
).
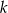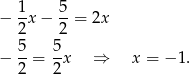
Zatem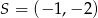 
. Skoro jest to środek odcinka o końcach 
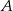i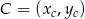 
, to mamy
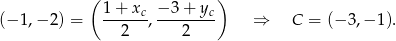
Pozostało obliczyć pole kwadratu. Policzmy długość przekątnej:
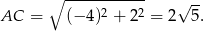
Możemy z tego obliczyć bok kwadratu, ale możemy też od razu skorzystać ze wzoru na pole rombu z przekątnymi:
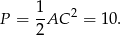
Odpowiedź: 
