/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9191470

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole trójkąta ograniczonego prostą 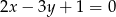2x − 3y + 1 = 0 i osiami układu współrzędnych.

Rozwiązanie

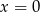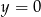Możemy zacząć od naszkicowania jak wygląda podana prosta. Aby to zrobić znajdziemy jej punkty wspólne z osiami układu współrzędnych. Wstawiamy do równania kolejno x = 0 i y = 0 . Daje nam to odpowiednio

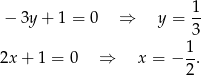
− 3y + 1 = 0 ⇒ y = 1- 3 1 2x + 1 = 0 ⇒ x = − -. 2

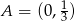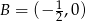Podana prosta przecina więc osie układu w punktach A = (0, 1) 3 i 1 B = (− 2,0) . Możemy teraz naszkicować obrazek.

PIC

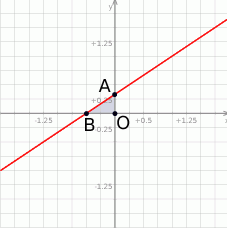
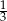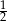Gdy to zrobimy to widać, że trójkąt, o który nam chodzi to trójkąt prostokątny o przyprostokątnych długości 13 i 12 . Zatem jego pole jest równe

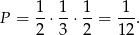
1- 1- 1- -1- P = 2 ⋅3 ⋅ 2 = 1 2.

 
Odpowiedź: -1 12

Wersja PDF