Zadanie nr 9256129
Wyznacz równanie prostej przechodzącej przez punkt 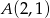 i tworzącej z prostą
i tworzącej z prostą 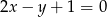 kąt o mierze
kąt o mierze 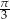 .
.
Rozwiązanie
zacznijmy od szkicowego rysunku.
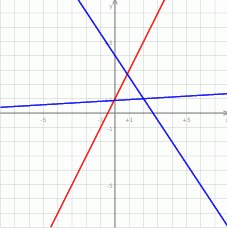
Dana prosta tworzy z osią 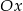 kąt
kąt  , którego tangens jest równy
, którego tangens jest równy 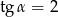 (współczynnik kierunkowy prostej). Szukamy zatem prostych, które tworzą z osią
(współczynnik kierunkowy prostej). Szukamy zatem prostych, które tworzą z osią 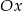 kąty
kąty 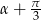 i
i 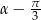 . Aby wyliczyć współczynniki kierunkowe tych prostych korzystamy ze wzorów
. Aby wyliczyć współczynniki kierunkowe tych prostych korzystamy ze wzorów
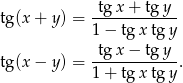
W naszej sytuacji mamy
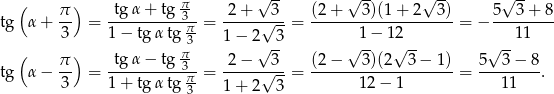
Znamy zatem współczynniki kierunkowe szukanych prostych 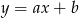 . Pozostało wyliczyć współczynnik
. Pozostało wyliczyć współczynnik 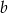 – robimy to podstawiając podany punkt.
– robimy to podstawiając podany punkt.
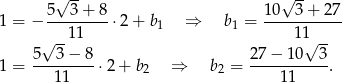
Odpowiedź: 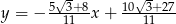 oraz
oraz