/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9276931

Dodaj do ulubionych
Dodaj do rozwiązanych

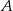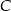Wierzchołki A i C kwadratu 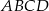ABCD o polu 8 leżą na prostej o równaniu 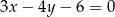3x − 4y − 6 = 0 . Środek symetrii tego kwadratu ma współrzędne 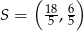( ) S = 18-, 6 5 5 . Oblicz współrzędne punktów 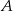A i C .

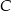Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

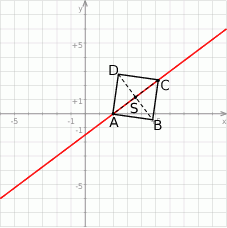
Zapiszmy równanie danej prostej w postaci kierunkowej.

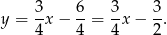
y = 3-x− 6-= 3x − 3-. 4 4 4 2

Wiemy, że bok kwadratu 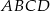ABCD jest równy 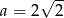√ -- a = 2 2 , więc

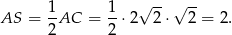
1 1 √ -- √ -- AS = -AC = --⋅2 2 ⋅ 2 = 2. 2 2

Szukamy więc punktów 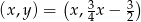( 3 3) (x,y) = x ,4x − 2 prostej 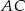AC , które są odległe od 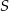S o 2.

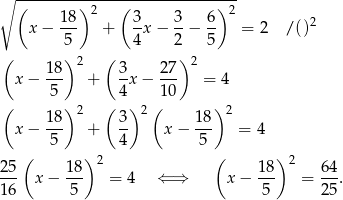
∘ (-------)-2---(------------)-2- 18- 3- 3- 6- 2 x− 5 + 4x − 2 − 5 = 2 / () ( ) ( ) 18- 2 3- 2-7 2 x− 5 + 4x − 1 0 = 4 ( ) 2 ( ) 2( ) 2 18- 3- 18- x− 5 + 4 x − 5 = 4 ( ) 2 ( ) 2 25- 18- 18- 6-4 16 x − 5 = 4 ⇐ ⇒ x− 5 = 2 5.

Mamy stąd

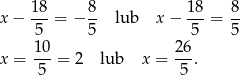
18 8 18 8 x − ---= − -- lub x − ---= -- 5 5 5 5 x = 10-= 2 lub x = 26. 5 5

Obliczamy jeszcze odpowiadające tym wartościom 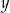y –ki.

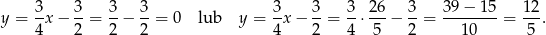
y = 3-x− 3-= 3− 3-= 0 lub y = 3x − 3-= 3-⋅ 26-− 3-= 39-−-15-= 12-. 4 2 2 2 4 2 4 5 2 10 5

 
Odpowiedź: 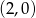(2,0) i ( ) 26, 12 5 5

Wersja PDF