Zadanie nr 9319984
Dane są punkty 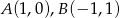 . Punkt
. Punkt 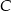 należy do okręgu o równaniu
należy do okręgu o równaniu 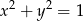 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu  tak, aby pole trójkąta
tak, aby pole trójkąta 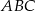 było największe. Oblicz to pole.
było największe. Oblicz to pole.
Rozwiązanie
Zacznijmy od szkicowego rysunku.
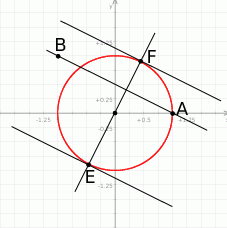
Korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty 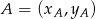 i
i 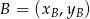 :
:
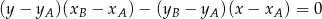
wyznaczamy równanie prostej 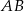
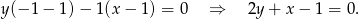
Ponieważ bok 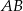 szukanego trójkąta jest ustalony i ma długość
szukanego trójkąta jest ustalony i ma długość
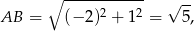
więc musimy znaleźć na okręgu punkty, którego odległość od prostej 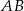 jest największa. Powinno być jasne, że taki punkt otrzymamy przecinając okrąg z prostą
jest największa. Powinno być jasne, że taki punkt otrzymamy przecinając okrąg z prostą 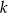 prostopadłą do
prostopadłą do 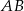 i przechodzącą przez środek okręgu (mówiąc inaczej, szukamy punktów, w których styczna do okręgu jest równoległa do
i przechodzącą przez środek okręgu (mówiąc inaczej, szukamy punktów, w których styczna do okręgu jest równoległa do 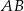 ).
).
Ponieważ prosta 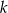 ma być prostopadła do
ma być prostopadła do 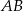 i przechodzić przez
i przechodzić przez 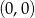 , więc ma równanie
, więc ma równanie 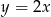 . Szukamy teraz jej punktów wspólnych z okręgiem (wstawiamy do równania okręgu).
. Szukamy teraz jej punktów wspólnych z okręgiem (wstawiamy do równania okręgu).
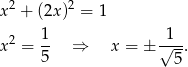
Daje to nam dwa punkty 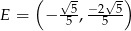 i
i 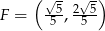 Widać z obrazka, że interesujący nas punkt to
Widać z obrazka, że interesujący nas punkt to 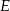 , ale jeżeli nie zrobiliśmy obrazka, lub nie jest on zbyt dokładny, to możemy sprawdzić, który z nich jest dalej od prostej
, ale jeżeli nie zrobiliśmy obrazka, lub nie jest on zbyt dokładny, to możemy sprawdzić, który z nich jest dalej od prostej 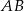 ze wzoru na odległość punktu od prostej.
ze wzoru na odległość punktu od prostej.
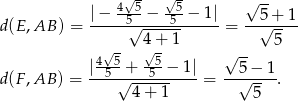
Bierzemy zatem 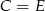 i pole jest równe
i pole jest równe
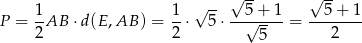
Odpowiedź: 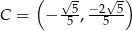 ,
,