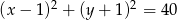/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9385737

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest odcinek o końcach 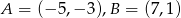A = (− 5,− 3),B = (7,1) .

  • Wyznacz równanie symetralnej tego odcinka.
  • Wyznacz równanie okręgu o średnicy AB .

Rozwiązanie

Rozpoczynamy od schematycznego rysunku.

PIC

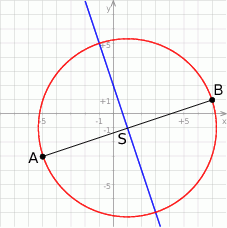
Wyznaczamy współrzędne środka odcinka 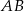AB

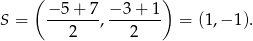
( ) S = −-5-+-7, −-3-+-1 = (1,− 1). 2 2
  • Wyznaczmy równanie prostej przechodzącej przez punkty A,B
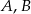
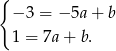
    { − 3 = −5a + b 1 = 7a+ b.

    Odejmijmy stronami te równania

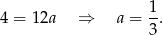
    4 = 12a ⇒ a = 1. 3

    Zatem

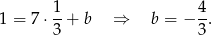
    1 4 1 = 7 ⋅--+ b ⇒ b = − --. 3 3

    Stąd prosta zawierająca punkty 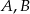A ,B ma równanie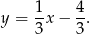

    y = 1x − 4. 3 3

    Wyznaczamy współczynnik kierunkowy symetralnej

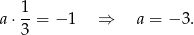
    1 a ⋅--= − 1 ⇒ a = − 3. 3

    Symetralna przechodzi przez środek odcinka, więc

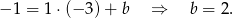
    −1 = 1⋅ (− 3 )+ b ⇒ b = 2.

    Zatem symetralna ma równanie

    y = − 3x + 2 .

     
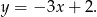
    Odpowiedź: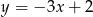 y = − 3x + 2

  • Mamy już wyznaczony środek okręgu pozostaje tylko policzyć długość promienia. Punkt 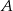A leży na szukanym okręgu więc jego odległość od środka jest równa długości promienia. Liczymy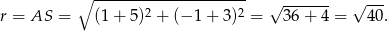
    ∘ --------------------- √ ------- √ --- r = AS = (1+ 5)2 + (− 1+ 3 )2 = 36+ 4 = 40.

    Zatem równanie szukanego okręgu ma postać

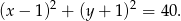
    (x − 1)2 + (y + 1)2 = 40.

     
    Odpowiedź: (x − 1)2 + (y + 1)2 = 40

Wersja PDF