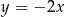/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9387973

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 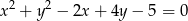x2 + y2 − 2x + 4y − 5 = 0 .

Rozwiązanie

Rozpocznijmy od wyznaczenia środka podanego okręgu (zwijamy do pełnych kwadratów).

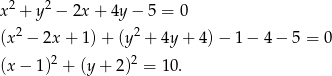
2 2 x + y − 2x + 4y − 5 = 0 (x2 − 2x + 1 )+ (y 2 + 4y + 4 )− 1 − 4 − 5 = 0 (x − 1)2 + (y + 2)2 = 1 0.

Zatem środek okręgu ma współrzędne 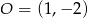O = (1,− 2) . Proste przechodzące przez początek układu współrzędnych mają postać 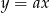y = ax . Współczynnik a wyznaczamy podstawiając współrzędne punktu O .

− 2 = a.

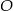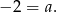
Na koniec obrazek.

PIC

 
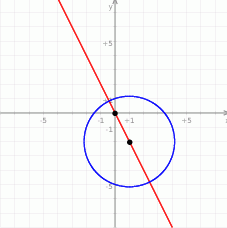
Odpowiedź: y = −2x

Wersja PDF