/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9390150

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że trójkąt o wierzchołkach 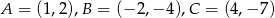A = (1 ,2 ),B = (− 2,− 4),C = (4,− 7) jest trójkątem prostokątnym.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

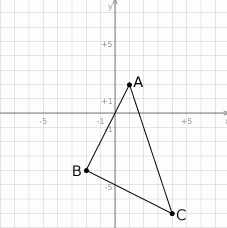
Sposób I

Liczymy długości boków trójkąta i korzystamy z twierdzenia odwrotnego do twierdzenia Pitagorasa.

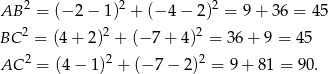
AB 2 = (− 2− 1)2 + (− 4− 2 )2 = 9+ 36 = 45 2 2 2 BC = (4+ 2) + (−7 + 4) = 36+ 9 = 45 AC 2 = (4 − 1)2 + (− 7− 2)2 = 9 + 81 = 90 .

Widać zatem, że

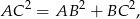
AC 2 = AB 2 + BC 2,

czyli kąt przy wierzchołku 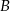B jest prosty.

Sposób II

Wyznaczymy proste zawierające boki trójkąta i sprawdzimy czy któreś są prostopadłe. Skorzystamy ze wzoru na prostą przechodzącą przez dwa punkty 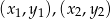(x1,y 1),(x 2,y2)

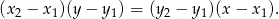
(x2 − x1)(y − y1) = (y2 − y1)(x − x 1).

Liczymy

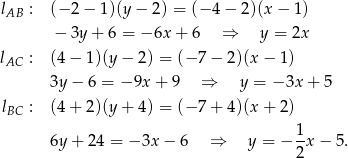
lAB : (− 2 − 1)(y − 2) = (− 4 − 2)(x − 1) − 3y + 6 = − 6x + 6 ⇒ y = 2x l : (4 − 1)(y − 2) = (− 7 − 2)(x − 1 ) AC 3y − 6 = −9x + 9 ⇒ y = − 3x + 5 l : (4 + 2)(y + 4) = (− 7 + 4)(x + 2 ) BC 6y + 24 = − 3x− 6 ⇒ y = − 1x − 5. 2

Sprawdzamy które są prostopadłe

( ) 2⋅ − 1- = − 1. 2

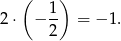
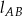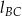Zatem proste lAB i lBC są prostopadłe, czyli kąt 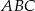ABC jest kątem prostym.

Wersja PDF