/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9407283

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku 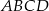ABCD dane są wierzchołki 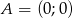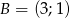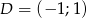A = (0;0) , B = (3;1) , D = (− 1;1) . Wyznacz wierzchołek 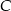C oraz środek symetrii tego równoległoboku.

Rozwiązanie

Możemy narysować podane punkty.

PIC

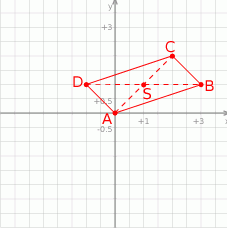
Sposób I

Łatwo wyznaczyć środek symetrii równoległoboku, czyli punkt przecięcia się jego przekątnych – jest to środek odcinka 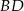BD .

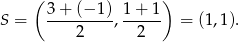
( ) S = 3-+-(−-1), 1-+-1 = (1,1). 2 2

Współrzędne punktu 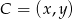C = (x,y) wyznaczamy korzystając z tego, że punkt 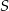S jest środkiem odcinka AC .

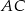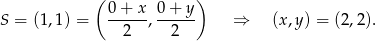
( ) 0 + x 0+ y S = (1,1) = ------,------ ⇒ (x ,y) = (2,2). 2 2

Sposób II

Niech 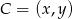C = (x,y ) . Mamy wtedy

→ → AB = DC [3,1] = [x + 1,y − 1].

Mamy stąd 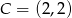C = (2,2) .

Środek symetrii 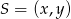S = (x,y) , to dokładnie punkt przecięcia się przekątnych, czyli koniec połowy wektora 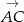→ AC zaczepionego w punkcie 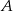A . Mamy zatem

→ 1 → AS = -AC 2 [x ,y ] = 1[2,2]. 2

Tak więc S = (1,1) .  
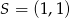Odpowiedź: C = (2,2), S = (1,1)

Wersja PDF