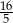Zadanie nr 9479175
Wyznacz odległość punktu 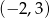 od prostej o równaniu
od prostej o równaniu 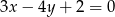 .
.
Rozwiązanie
Korzystamy ze wzoru na odległość punktu 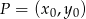 od prostej
od prostej 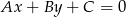 :
:
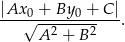
Otrzymujemy zatem
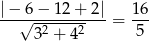
Odpowiedź: 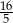
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz odległość punktu 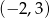 od prostej o równaniu
od prostej o równaniu 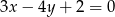 .
.
Korzystamy ze wzoru na odległość punktu 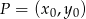 od prostej
od prostej 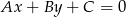 :
:
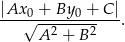
Otrzymujemy zatem
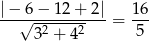
Odpowiedź: