/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9519789

Dodaj do ulubionych
Dodaj do rozwiązanych

Na prostej o równaniu 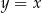y = x wyznacz współrzędne punktu 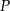P leżącego najbliżej punktu K = (− 1;7) .

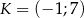Rozwiązanie

Niech 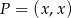P = (x ,x) będzie dowolnym punktem prostej 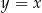y = x . Liczymy teraz kwadrat odległości KP .

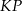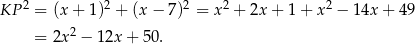
2 2 2 2 2 KP = (x+ 1) + (x − 7) = x + 2x + 1 + x − 14x + 49 = 2x2 − 12x + 50.

Musimy zatem wyznaczyć najmniejszą wartość funkcji 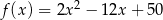2 f (x) = 2x − 12x + 5 0 . Ponieważ jest to parabola o ramionach skierowanych w górę, przyjmuje ona wartość najmniejszą w wierzchołku, czyli dla 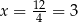x = 124-= 3 . Wtedy 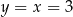y = x = 3 . Zatem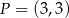 P = (3,3)

Na koniec możemy sobie naszkicować całą sytuację.

PIC

 
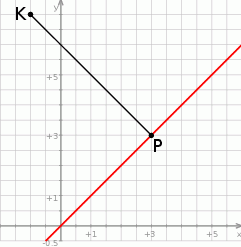
Odpowiedź: P = (3,3)

Wersja PDF