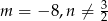/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9604115

Dodaj do ulubionych
Dodaj do rozwiązanych

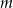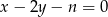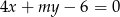Oblicz dla jakich wartości parametrów m i n proste o równaniach: x − 2y − n = 0 i 4x + my − 6 = 0 są dwiema różnymi prostymi równoległymi.

Rozwiązanie

Przekształćmy równania prostych

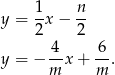
1 n y = -x − -- 2 2 y = − 4-x+ 6-. m m

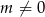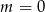Drugie przekształcenie ma oczywiście sens tylko, gdy m ⁄= 0 . Dla m = 0 druga prosta jest pionowa, więc na pewno nie jest równoległa do pierwsze prostej. Proste są równoległe, gdy mają takie same współczynniki kierunkowe, skąd otrzymujemy równanie

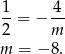
1 4 --= − -- 2 m m = − 8 .

Sprawdźmy jeszcze kiedy proste są różne. Ponieważ 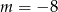m = −8 równania prostych mają postać:

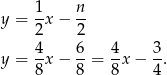
y = 1-x− n- 2 2 4 6 4 3 y = --x− --= -x − --. 8 8 8 4

Proste będą różne, gdy

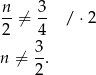
n 3 --⁄= -- / ⋅2 2 4 n ⁄= 3-. 2

 
Odpowiedź: m = − 8,n ⁄= 32

Wersja PDF