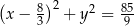Zadanie nr 9664891
Napisz równanie okręgu, którego środek należy do osi  , i który przechodzi przez punkty
, i który przechodzi przez punkty 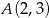 i
i 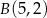 .
.
Rozwiązanie
Zaczynamy od rysunku.
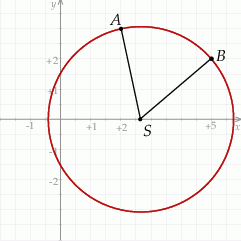
Szukamy punktu 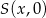 , który jest równo odległy od punktów
, który jest równo odległy od punktów 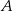 i
i 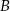 .
.
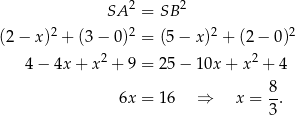
Zatem środek okręgu ma współrzędne 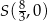 . Pozostało obliczyć jego promień.
. Pozostało obliczyć jego promień.
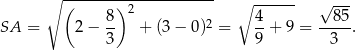
Możemy teraz napisać równanie okręgu
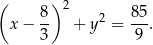
Odpowiedź: