Zadanie nr 9702276
Dana jest parabola o równaniu 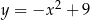 . Na tej paraboli leży punkt
. Na tej paraboli leży punkt 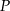 o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie
o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie 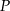 ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
Rozwiązanie
Szkicujemy opisaną sytuację.
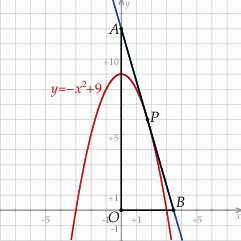
Niech 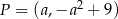 będzie punktem danej paraboli o współrzędnych dodatnich, tzn.
będzie punktem danej paraboli o współrzędnych dodatnich, tzn. 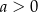 i
i
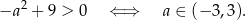
Liczymy pochodną danej funkcji kwadratowej.
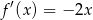
Styczna do paraboli w punkcie 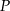 ma więc równanie
ma więc równanie
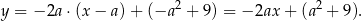
Wyznaczmy teraz punkty wspólne tej prostej z osiami układu współrzędnych. Punkt wspólny z osią 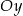 to
to 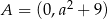 . Ponadto,
. Ponadto,
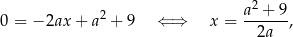
więc punkt przecięcia stycznej z osią 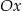 to
to
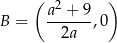
Pole trójkąta prostokątnego  jest równe
jest równe
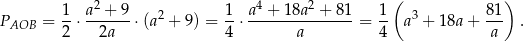
Przypomnijmy, że dziedziną tej funkcji jest przedział 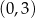 . Liczymy pochodną.
. Liczymy pochodną.
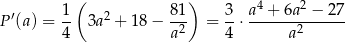
W liczniku mamy równanie dwukwadratowe – podstawiamy 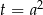 .
.
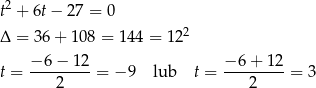
Pochodna funkcji 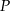 jest więc równa
jest więc równa
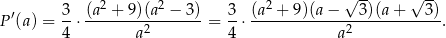
Widać teraz, że pochodna jest ujemna w przedziale 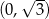 i dodatnia w przedziale
i dodatnia w przedziale 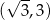 . To oznacza, że funkcja
. To oznacza, że funkcja 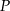 jest malejąca
jest malejąca 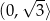 i rosnąca
i rosnąca 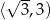 . To oznacza, że najmniejszą wartość pola trójkąta
. To oznacza, że najmniejszą wartość pola trójkąta 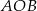 otrzymamy dla
otrzymamy dla 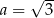 . Mamy wtedy
. Mamy wtedy
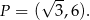
Odpowiedź: