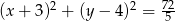/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9709094

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie okręgu o środku 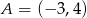A = (− 3,4) , stycznego do prostej o równaniu y = 3x + 1 .

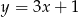Rozwiązanie

Skoro okrąg ma być styczny do podanej prostej, to jego promień musi być dokładnie równy odległości podanego środka 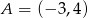A = (− 3,4) od danej prostej 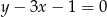y− 3x − 1 = 0 . Ze wzoru na odległość punktu od prostej mamy

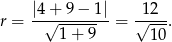
|4-+-9-−-1|- -12-- r = √ ------ = √ --. 1 + 9 10

Zatem szukane równanie okręgu ma postać

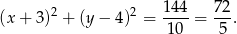
2 2 144 72 (x+ 3) + (y− 4) = -10-= -5-.

Na koniec obrazek.

PIC

 
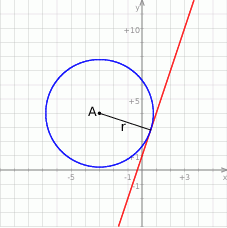
Odpowiedź: (x + 3)2 + (y − 4)2 = 725-

Wersja PDF