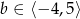Zadanie nr 9730580
Dany jest prostokąt o wierzchołkach 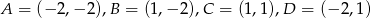 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika 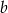 , dla których prosta o równaniu
, dla których prosta o równaniu 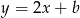 ma co najmniej jeden punkt wspólny z prostokątem
ma co najmniej jeden punkt wspólny z prostokątem 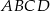 .
.
Rozwiązanie
Najważniejszy jest rysunek.
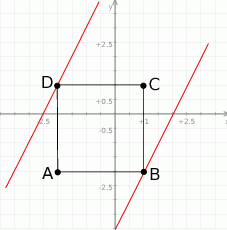
Wszystkie proste postaci 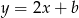 są równoległe – współczynnik
są równoległe – współczynnik 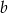 decyduje tylko o tym w jakim punkcie prosta ta przecina oś
decyduje tylko o tym w jakim punkcie prosta ta przecina oś 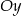 . Z naszkicowanego rysunku widać, że dwa skrajne położenia takiej prostej mamy gdy przechodzi ona przez wierzchołki
. Z naszkicowanego rysunku widać, że dwa skrajne położenia takiej prostej mamy gdy przechodzi ona przez wierzchołki 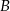 i
i 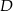 – dla pośrednich wartości
– dla pośrednich wartości 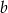 , proste przecinają prostokąt. Sprawdźmy kiedy prosta
, proste przecinają prostokąt. Sprawdźmy kiedy prosta 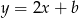 przechodzi przez punkty
przechodzi przez punkty 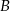 i
i 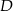 .
.
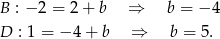
Odpowiedź: