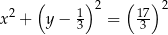/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9757997

Dodaj do ulubionych
Dodaj do rozwiązanych

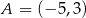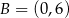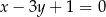Wyznacz równanie okręgu przechodzącego przez punkty A = (− 5,3) i B = (0,6) , którego środek leży na prostej o równaniu x− 3y + 1 = 0 .

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

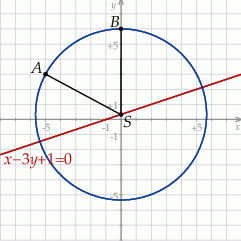
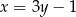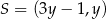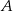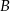Wyznaczmy najpierw środek szukanego okręgu. Wiemy, że leży on na prostej x = 3y − 1 , więc ma współrzędne postaci S = (3y − 1,y) . Punkt ten musi być równo odległy od punktów A i B – zapiszmy ten warunek.

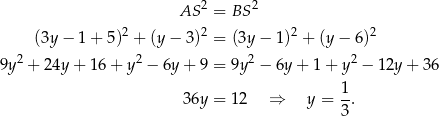
AS 2 = BS2 (3y − 1+ 5 )2 + (y − 3)2 = (3y− 1)2 + (y− 6)2 2 2 2 2 9y + 24y + 16 + y − 6y + 9 = 9y − 6y+ 1+ y − 12y + 36 1- 36y = 12 ⇒ y = 3.

Zatem środek okręgu ma współrzędne 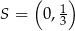( 1) S = 0,3 . Pozostało obliczyć jego promień.

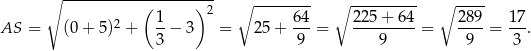
∘ --------------------- ∘ -------- ∘ --------- ∘ ---- ( 1 ) 2 64 225 + 64 2 89 1 7 AS = (0 + 5)2 + --− 3 = 25 + ---= ---------= ---- = ---. 3 9 9 9 3

Możemy teraz napisać równanie okręgu

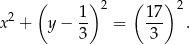
( 1) 2 ( 17) 2 x2 + y− -- = --- . 3 3

 
Odpowiedź: ( 1)2 (17) 2 x2 + y− 3 = -3

Wersja PDF