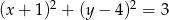/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9887862

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie okręgu, który jest obrazem okręgu 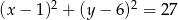2 2 (x − 1) + (y − 6) = 2 7 w jednokładności o środku 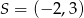S = (− 2,3) i skali 13 .

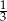Rozwiązanie

Możemy na początek naszkicować sobie o co chodzi. Trudno o dokładny rysunek, ale szkic powinien nam wystarczyć.

PIC

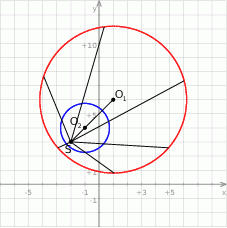
Ponieważ promień okręgu zmienia się jak skala jednokładności, szukany okrąg będzie miał promień

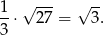
--- -- 1-⋅√ 27 = √ 3 . 3

Pozostało wyznaczyć jego środek. Nie jest to trudne, jeżeli 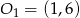O 1 = (1,6 ) jest środkiem danego okręgu, a 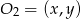O2 = (x ,y) środkiem okręgu, którego szukamy, to mamy równość

−→ 1-−→ SO 2 = 3 SO 1 1 [x+ 2,y − 3] = --[1 + 2,6 − 3] = [1,1] { 3 x + 2 = 1 ⇒ x = − 1 y − 3 = 1 ⇒ y = 4.

Zatem równanie szukanego okręgu to

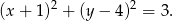
(x + 1)2 + (y − 4)2 = 3.

 
Odpowiedź: (x + 1)2 + (y − 4)2 = 3

Wersja PDF